| ѕример | оличество устран€емых гипотез |
| 1. ѕоложительный, совпадающий с первым по одному признаку ќтрицательный, совпадающий с первым по одному признаку | |
| 2. ѕоложительный, совпадающий с первым по двум признакам ќтрицательный, совпадающий с первым по двум признакам | |
| 3. ѕоложительный, совпадающий с первым по трем признакам ќтрицательный, совпадающий с первым по трем признакам | |
| 4. ќтрицательный, различающийс€ с первым по четырем признакам |
»з табл. 2 видно, что на втором шаге работы испытуемого различные типы встречаемых им примеров существенно различаютс€ по числу гипотез, которые они позвол€ют устранить при рациональной работе испытуемого. Ќаиболее Ђинформативнымиї €вл€ютс€ примеры первого типа Ц такой пример позвол€ет устранить все гипотезы, кроме одной, и, таким образом, уже на втором шаге отгадать задуманное пон€тие. Ќаименее информативными, пустыми, оказываютс€ отрицательные примеры первого типа Ц они не позвол€ют устран€ть ни одной гипотезы. Ћегко заметить, что пустых или комплементарных положительных примеров быть уже не может.
Ќа очередном, третьем шаге работы испытуемый может встретить уже только три типа примеров, совпадающих/различающихс€ по одному или двум признакам, а также пустые. ѕричем встреча с положительным примером, совпадающим, или с отрицательным, различающимс€ с первым по одному признаку, снова ведет к решению задачи. Ќаконец, на четвертом шаге испытуемый может встретитьс€ или с пустым примером, или же с примером, совпадающим/отличающимс€ по одному признаку, и, таким образом, даже в случае наиболее неблагопри€тных примеров на предыдущих шагах отгадать задуманное экспериментатором пон€тие. »наче говор€, если не считать пустых примеров, рационально действующий испытуемый непременно решит задачу за четыре шага. Ёто и есть минимальное Ђлогически необходимоеї число непустых примеров, которое гарантирует уверенное решение задачи даже в наиболее неблагопри€тном случае.
»деальные и реальные стратегии. »з разбора шагов, ведущих к последовательному сокращению числа альтернативных гипотез, можно увидеть, что всегда существует некотора€ идеальна€ (рациональна€) стратеги€, с необходимостью привод€ща€ к решению поставленной задачи. ¬ данном случае нетрудно было опознать стратегию фокусировки. Ѕыло бы неверным, однако, считать, что это единственна€ идеальна€ стратеги€, ведуща€ к решению задачи, или даже что она наиболее эффективна в любом случае. ѕрименение вс€кой идеальной стратегии позвол€ет достигать конкретных целей, которыми (в разных случа€х) могут становитьс€: 1) максимизаци€ получаемой информации; 2) снижение нагрузки на пам€ть и логическое членение; 3) образование данного пон€ти€ за минимальное число шагов; 4) сведение к минимуму числа ошибочных гипотез в процессе образовани€ пон€ти€; 5) достижение субъективной уверенности в правильном образовании пон€ти€ вне зависимости от числа примеров, с которыми встретилс€ испытуемый, и др.
ѕон€тие идеальных стратегий €вл€етс€ средством анализа и описани€ реальной работы испытуемого в эксперименте. ќно не только задает единицу анализа процесса образовани€ пон€ти€, позвол€€ рассматривать отдельные шаги этого процесса как необходимые и несамосто€тельные моменты целого, но также открывает путь дл€ исследовани€ разнообразных зависимостей, существующих между отдельными составл€ющими ситуации.
|
|
|
“ипы реальных стратегий представл€ют собой качественные значени€ зависимой переменной в экспериментах по образованию искусственных пон€тий. ”мение правильно идентифицировать рассмотренные стратегии €вл€етс€ критерием освоени€ методики Ѕрунера. ≈сли цель достигнута, можно приступить к постановке и решению собственно исследовательских вопросов о факторах, определ€ющих выбор той или иной стратегии. ѕример такого использовани€ методики в исследовательских цел€х дает задание є 11 в разделе ЂЁкспериментальный методї исследовательского практикума.
Ћитература: 10; 15.
«адание 12. »спользование теории информации в модифицированном варианте методики образовани€ искусственных пон€тий
“ема задани€
«накомство с модификацией методики образовани€ искусственных пон€тий, предложенной ќ. . “ихомировым.
¬ведение
»нформаци€ как количественное пон€тие имеет смысл только как результат осуществлени€ какогоЦлибо событи€, имеющего некоторую веро€тность. ¬еро€тностные же свойства объектов в экспериментах ƒж. Ѕрунера не анализировались и не €вл€лись предметом исследовани€. Ёксперименты проводились с испытуемыми однократно. ÷елью их было только посмотреть, какую стратегию выберет испытуемый в зависимости от варьировани€ некоторых условий. ¬ таком эксперименте, естественно, нельз€ было ставить вопрос о том, могут ли испытуемые прийти к оптимальной в соответствующих услови€х стратегии в результате тренировки, какими факторами обусловливаетс€ изменение стратегий.
ƒл€ того чтобы ответить на эти вопросы, необходимо было изменить методику таким образом, чтобы испытуемый находилс€ в ситуации выбора различных информативных элементов в течение длительного времени, что достигаетс€ многократным предъ€влением ему ограниченного набора задач. ѕри таких услови€х оказываетс€ возможным вы€снить, чем обусловливаетс€ его поискова€ де€тельность, вскрыть факторы, определ€ющие и регулирующие ее осуществление.
ћодификаци€ методики ќ. . “ихомировым. —оответствующа€ методика была предложена ќ. . “ихомировым. «адачей исследований ќ. . “ихомирова [1969] €вл€лось изучение закономерности самосто€тельного решени€ человеком задач с неопределенностью, т.е. задач, решение которых может заканчиватьс€ различным результатом, и следовательно, до нахождени€ решени€ существует известна€ неопределенность относительно конечного результата задач на распознавание €влений.
ƒл€ этой цели было применено сопоставление хода реального процесса решени€ мыслительной задачи на классификацию с оптимальным способом ее решени€, выводимым на основании специальных математических расчетов, в результате чего оказываетс€ возможным получить некоторую характеристику реального процесса.
»спользованна€ методика была во многих отношени€х сходной с методикой образовани€ искусственных пон€тий в варианте ¬ыготскогоЦ—ахарова. » в том, и в другом случае задача испытуемого заключаетс€ в нахождении методом последовательных проб принципа классификации, избранного экспериментатором. ≈сли же рассматривать группы объектов, которые в результате классификации должен был выделить испытуемый по аналогии с образованием искусственных пон€тий (определение каждой группы рассматривать как образование искусственного пон€ти€), то основное отличие данной методики от методики ¬ыготскогоЦ—ахарова заключаетс€ в том, что основание такой классификации €вл€етс€ переменным, Ц центральный момент методики ќ. . “ихомирова. »менно переменный характер классификации объектов позволил использовать дл€ описани€ оптимальных способов решени€ задач методы теории веро€тности и теории информации, так как это приводило к созданию статистической характеристики обследуемых объектов. — описанной модификацией методики ¬ыготскогоЦ—ахарова студенты должны ознакомитьс€ в насто€щем задании.
|
|
|
÷ель задани€ Ц применить использование теории информации дл€ изучени€ процесса образовани€ искусственных пон€тий.
—татистическа€ структура обследуемого пол€. ¬ методику входит весь набор стимульного материала, и указаны наборы карточек, которые рекомендуетс€ использовать в опытах.
¬ качестве наборов гипотез предлагаетс€ рассмотреть те 3 набора, которые представлены ниже, в разделе ЂЁкспериментальный материалї с 2, 4 и 14 объектами в группе.
ѕри заданных услови€х в длинном р€ду предъ€влений стимульных объектов (карточек) (рис. 12) кажда€ гипотеза может реализоватьс€ (соответствовать предъ€вл€емым карточкам) в среднем одинаковое число раз. —ледовательно, веро€тность реализации дл€ каждой гипотезы равна: дл€ I набора –1 = – 2= 1/2; дл€ II набора – 1= – 2= – 3= – 4= 1/4; дл€ III набора –1 = – 2= – 3 =... = – 14 = 1/14. ќчевидно, что чем больше возможных исходов, предъ€вл€емых испытуемому дл€ распознавани€ гипотез, тем более неопределенен конечный исход решени€. »спользу€ теорию информации, можно выразить неопределенность опыта более точно. ¬ теории информации показано, что неопределенность опыта Ц Ќ, или энтропи€, Ц €вл€етс€ функцией числа возможных исходов и веро€тности их реализации:
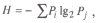
где – Ц веро€тность отдельного исхода опыта. ≈сли исходы равноверо€тны, то Ќ = lg2 M, где ћ Ц число возможных исходов опыта.
“аким образом, услови€ разбираемой нами задачи будут описыватьс€ так: 1) Ќ= lg22 = 1 дв. ед.; 2) Ќ= lg24 = 2 дв. ед.; 3) ЌЦ lg214 = 4 дв. ед. ¬ прин€тых услови€х эксперимента каждый из объектов, помимо своих посто€нных признаков Ц количества фигур, нарисованных на карточках, их цвета, формы и фона (или числа каемок), приобретает совершенно определенную статистическую характеристику частоты, с которой этот объект оказываетс€ вход€щим в искомую группу при многократном решении задач. ¬се объекты, таким образом, распредел€ютс€ на две категории: объекты, которые никогда не вход€т в искомую группу; объекты, которые всегда вход€т в группу с веро€тностью больше нул€, но меньше единицы. ¬ св€зи с тем что объекты помимо своих посто€нных признаков в прин€тых услови€х приобретают еще один переменный признак (вхождени€ или невхождени€ в искомую группу), каждую отдельную пробу следует рассматривать также как опыт, могущий иметь несколько различных исходов с различной веро€тностью их реализации и, следовательно, характеризующийс€ неопределенностью:
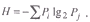
“аким образом, процесс решени€ задачи выступает как процесс последовательного обследовани€ пол€, имеющего некоторую статистическую характеристику, а отдельные пробы могут относитьс€ к объектам с различной энтропией по€влени€ провер€емого признака. ѕоскольку получаема€ информаци€ равна уменьшению исходной неопределенности: I = H 1 Ц Ќ2, результаты проверки различных объектов могут различатьс€ по их информативности. ѕрименим теперь тот же метод к анализу второй пробы с учетом одного осложн€ющего услови€: если перед первой пробой дл€ каждой программы статистическа€ характеристика обследуемого пол€ €вл€етс€ посто€нной, то перед вторым выбором распределение веро€тностей получени€ Ђдаї дл€ всех объектов пол€ зависит от результатов предшествующего выбора, т.е. имеет место некоторое распределение условных веро€тностей.
|
|
|
ѕоскольку отдельные пробы имеют различную информативность, множество различных способов решени€ данной задачи можно оценивать по тому, как соотнос€тс€ необходима€ и избыточна€ информации, собираемые испытуемым, дл€ решени€ этой задачи при применении различных способов.
ѕри распознавании гипотез в одном наборе оптимальным способом поиска будет выбор любого объекта с веро€тностью получени€ положительного ответа 0,5, дающий информацию, равную 1 дв. ед. ѕри распознавании гипотез во втором наборе оптимальным способом поиска будет €вл€тьс€ последовательный выбор двух объектов, дающий каждый соответственно по 1 дв. ед.
ћетодика
ќпыт состоит из 2 частей: 1) с расположением объектов, данном в ѕриложении; 2) с измененным (произвольно) пор€дком карточек, но с тем же набором гипотез.
ѕолученные данные должны быть использованы дл€ ответов на следующие вопросы:
♦ ак вли€ет неопределенность условий задачи на ход ее решени€?
♦ ак протекает обследование пол€ до вы€влени€ его статистической характеристики и после?
♦ ¬ли€ет ли пространственное расположение объектов на протекание поиска?
Ёкспериментальный материал. ¬ эксперименте используетс€ набор объектов (81 шт.): карточки белого, желтого и зеленого цветов, на которых изображены геометрические фигуры разной формы Ц квадраты, треугольники, кружки; все они разного цвета Ц черные, красные или синие в разном количестве по 1, 2, 3. ѕолный комплект карточек (81 шт.) раскладываетс€ перед испытуемым в таком пор€дке, как они представлены на вкладке (см. рис. 12). Ёкспериментатором заранее составл€ютс€ некоторые наборы гипотез и соответствующих им объектов, составл€ющих определенную группу, которые будут предложены испытуемому дл€ распознавани€, т.е. дл€ образовани€ экспериментального пон€ти€.
¬озможные наборы гипотез:
I
1. 3 квадрата
2. 3 черные фигуры
II
1. 3 квадрата
2. 3 черные фигуры
3. ¬се черные фигуры
4. ¬се черные фигуры на белом фоне
III
1. вадраты
2. „ерные фигуры
3. 3 фигуры
4. ‘игуры на белом фоне
5. 3 квадрата
6. 3 черные фигуры
7. „ерные фигуры на белом фоне
8. вадраты на белом фоне
9. 3 фигуры на белом фоне
10. „ерные квадраты
11.3 черных квадрата
12. 3 квадрата на белом фоне
13. „ерные квадраты на белом фоне
14. 3 черные фигуры на белом фоне
¬виду трудоемкости вычислений и значительного времени, которого требует проведение данного опыта, в особенности с предъ€влением дл€ распознавани€ испытуемому набора, состо€щего из 14 гипотез, последний приводитс€ здесь дл€ иллюстрации; студенты могут ограничитьс€ предъ€влением лишь первых двух наборов гипотез или не доводить поиск в случае предъ€влени€ 14 гипотез до оптимального способа.
ѕодготовка экспериментального материала включает также следующий этап: использу€ таблицу случайных чисел, экспериментатор составл€ет последовательность предъ€влени€ испытуемым каждой гипотезы (в случайном пор€дке); каждой соответствует определенный набор объектов (20 предъ€влений к I и II набору и 28 предъ€влений к III набору). ¬ случае если за такое количество времени испытуемым не находитс€ оптимальный способ решени€ данной задачи, экспериментатор начинает задавать гипотезы снова в том же пор€дке. »спытуемый не должен знать, какие гипотезы и сколько раз могут быть предъ€влены ему дл€ распознавани€.
ќтработка задани€
ќпыт проводитс€ с одним испытуемым первоначально с набором из 2 гипотез, а затем, после перехода испытуемого в этом случае к оптимальному поиску, экспериментатор без предупреждени€ переходит к предъ€влению дл€ распознавани€ набора из 4 гипотез. ¬есь опыт продолжаетс€ до тех пор, пока испытуемый не начинает стабильно, в течение р€да задач (6Ц8), определ€ть в каждом случае требуемую гипотезу, использу€ оптимальную стратегию поиска. ѕробы, делаемые испытуемым в процессе опыта, регистрируютс€ на специальном бланке, кажда€ клетка которого соответствует определенному объекту (карточке) из всего набора, предлагаемого испытуемому. Ёкспериментатор отмечает номер сделанного испытуемым выбора на бланке. аждый такой бланк €вл€етс€ протоколом решени€ испытуемым каждой отдельной задачи Ц распознавани€ задуманной группы объектов в каждом конкретном случае. Ќа бланкеЦпротоколе об€зательно фиксируютс€ номера задач. ќбразец бланка с зафиксированным ходом опыта дан в ѕриложении.
|
|
|
¬ каждой части опыта участвуют экспериментатор и один испытуемый. ¬с€ группа испытуемых делитс€ на две подгруппы Ц дл€ участи€ в первой и второй част€х опыта.
»нструкци€ испытуемому: Ђѕеред вами расположен набор объектов (карточек), характеризующихс€ различными признаками. Ёкспериментатор задумывает некоторую группу этих объектов. ¬ам предстоит определить, что это за группа. ƒл€ этого ¬ы можете указать на любой объект и спросить экспериментатора, входит ли он в задуманную группу карточек. ѕодобные выборы объектов осуществл€йте до тех пор, пока ¬ам не станет €сно, какую группу объектов задумал экспериментатор. ¬ы должны назвать эту группу. ≈сли ответ экспериментатора окажетс€ отрицательным, продолжайте поиск. —тарайтесь при нахождении требуемой группы делать как можно меньше проб отдельных объектовї.
ѕоследнее требование инструкции повтор€етс€ часто, перед решением почти каждой задачи, пока испытуемый не перейдет к оптимальному поиску с минимальным числом проб.
ќбработка результатов
ƒл€ получени€ данных в цел€х ответа на первый вопрос требуетс€ подсчитать общее количество решенных задач, предшествующее устойчивому осуществлению испытуемыми оптимального поиска в случае предъ€влени€ первого и второго набора гипотез.
ак уже указывалось, оптимальным способом поиска дл€ I набора гипотез будет опробование любой карточки с веро€тностью получени€ положительного ответа 1/2. ƒл€ II набора гипотез необходимо опробовать уже две карточки: первую Ц с веро€тностью получени€ ответа Ђдаї Ц 1/2, и вторую, веро€тность получени€ ответа Ђдаї которой будет 1/2 после осуществлени€ первого выбора.
¬ табл. 1 показано распределение веро€тностей получени€ положительного ответа дл€ I набора гипотез при расположении карточек первой части опыта.
ƒл€ получени€ данных по второму вопросу требуетс€ проследить, каким образом испытуемый осуществл€ет поиск в каждой конкретной задаче, дл€ чего требуетс€ подсчитать количество информации, получаемой им при осуществлении каждого выбора.
ѕри предъ€влении I набора гипотез это делаетс€ просто, так как из приведенных выше формул €сно, какое количество информации получает испытуемый в каждом выборе. Ёкспериментатор должен фиксировать, на каком этапе испытуемым получена требуема€ информаци€ 1 дв. ед. и как долго продолжаетс€ после этого последующий поиск. ѕри каждом выборе в этом случае испытуемый будет получать нулевую информацию.
ѕри предъ€влении II набора гипотез дело несколько усложн€етс€, так как после первых выборов поЦразному будет измен€тьс€ статистическа€ характеристика обследуемого пол€, и экспериментатор должен сам научитьс€ ее определ€ть. ѕокажем на примере, как это делаетс€. ѕредположим, что испытуемый первым назвал объект Ђ3 синих круга на желтом фонеї. »з табл. 2 видно, что веро€тность получени€ положительного ответа при выборе этой карточки равна 0, и полученна€ информаци€, следовательно, тоже равна 0; статистическа€ характеристика пол€ остаетс€ неизменной.
ƒопустим теперь, что испытуемый назвал карточку Ђ3 черных квадрата на белом фонеї. ¬еро€тность получени€ положительного ответа в этом случае равна 1 и, следовательно, полученна€ информаци€ также равна 0 при неизменной статистической характеристике пол€. ¬озьмем, наконец, случай первого выбора испытуемым карточки, характеризующейс€ некоторой средней веро€тностью получени€ положительного ответа о принадлежности ее к задуманной группе, например карточки Ђ1 черный круг на белом фонеї. »з табл. 2 видно, что веро€тность ее равна 0,5. —ледовательно, при ее выборе испытуемый получает 1 дв. ед. информации. Ёкспериментатор должен рассуждать следующим образом: если ответ положительный, следовательно, искомыми могут оставатьс€ или группа Ђвсе черные фигурыї, или группа Ђчерные фигуры на белом фонеї, а группы Ђ3 квадратаї и Ђ3 черные фигурыї быть не могут. ≈сли же ответ отрицательный, напротив, остаютс€ возможными последние две гипотезы. »сход€ из этих соображений составл€етс€ нова€ статистическа€ характеристика пол€: при положительном ответе (табл. 3) и отрицательном ответе (табл. 4).
|
|
|
1. ћатрица веро€тностей получени€ ответа Ђдаї при проверке каждого объекта дл€ I набора гипотез

2. ћатрица веро€тностей получение ответа Ђдаї при проверке каждого объекта дл€ II набора гипотез
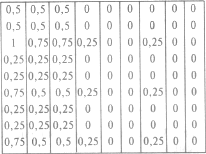
3. »змерение значений веро€тности получени€ ответа Ђдаї при проверке каждого объекта перед вторым выбором после получени€ положительного ответа на первый выбор (II набор гипотез)
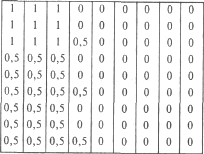
4. »змерение значений веро€тности получени€ ответа Ђдаї при проверке каждого объекта перед вторым выбором после получени€ отрицательного ответа на первый выбор (II набор гипотез)

Ёкспериментатор может не чертить в каждом случае новую статистическую характеристику пол€, а вычисл€ть устно получаемую информацию при каждом выборе. ƒанные о количестве информации, получаемой испытуемым при каждом выборе, занос€тс€ в табл. 19. ѕосле заполнени€ таблицы экспериментатором строитс€ график (дл€ первого выбора по I набору гипотез и дл€ первого и второго выбора в отдельности по II набору гипотез), на котором по горизонтальной оси откладываетс€ номер решаемой задачи, а на вертикальной оси Ц количество информации, полученной испытуемым (рис. 13).
 є задани€
є задани€
–ис. 13. √рафик изменени€ количества информации, получаемой испытуемым.
ќбсуждение результатов
Ќа основании полученных данных, конечным итогом которых €вл€етс€ динамика изменени€ количества информации, получаемой испытуемым в последовательно решаемых им задачах, следует сделать вывод о структуре поиска, о его соответствии или несоответствии статистической характеристике пол€, о факторах и услови€х, способствующих быстрейшему переходу испытуемого к оптимальному способу поиска при решении задач на распознавание.
онтрольные вопросы
1. ¬ чем заключаетс€ методика образовани€ искусственных пон€тий, разработанна€ јхом? аковы ее достоинства и недостатки?
2. аковы особенности методики двойной стимул€ции ¬ыготскогоЦ—ахарова?
3. аковы современные методики, изучающие процесс распознавани€ €влений, основывающиес€ на методике образовани€ искусственных пон€тий?
4. ак измен€етс€ статистическа€ структура обследуемого пол€ гипотез при последовательном выборе испытуемым положительных и отрицательных примеров?
Ћитература: 64.
ѕ–»Ћќ∆≈Ќ»≈
ќбразец бланка дл€ регистрации хода решени€ задач
«адача 1 «адача 2
–аздел 6. Ћ»„Ќќ—“№
І 15. ¬ведение к задани€м 13Ц14
ћетодики исследовани€ феноменов Ђуровень прит€занийї и Ђпресыщениеї были предложены в школе немецкого психолога урта Ћевина (1890Ц1947). . Ћевин одним из первых обратилс€ к экспериментальному исследованию мотивационной и целевой обусловленности поведени€ человека в конкретной обстановке (в Ђпсихологическом полеї). ќн считал, что поведение человека побуждают Ђквазипотребностиї. Ётим термином . Ћевин обозначал не биологические влечени€, а психологические образовани€, за которыми сто€т системы напр€жений в психологическом поле и которые возникают в том числе в св€зи с жизненными цел€ми человека. Ѕолее того, он подчеркивал, что цели и намерени€ сто€т по своим динамическим свойствам в одном р€ду с потребност€ми, что именно они (квазипотребности) специфичны дл€ человека.
¬ учении . Ћевина был поставлен вопрос о св€зи между потребностью и предметом, служащим дл€ ее удовлетворени€. ќн показал, что человек всегда существует в определенной конкретной ситуации, где кажда€ вещь, предмет выступают в отношении к потребност€м и стремлени€м человека, в том числе сами обладают Ђхарактером требовани€ї10. . Ћевин указывал на динамичность этих отношений, на то, что любое человеческое действие мен€ет Ђсоотношение сил в ситуацииї и поЦновому определ€ет результирующий вектор сил, направл€ющий поведение. ѕоэтому вс€кое экспериментальное психологическое исследование требует анализа взаимодействи€ человека с окружающей действительностью. . Ћевин подчеркивал, что человек всегда включен в окружающую его ситуацию, сама среда должна рассматриватьс€ в ее отношении к действующему человеку. Ѕ. ¬. «ейгарник обозначала это взаимодействие как Ђпласт жизненных отношенийї [«ейгарник, 1998].
ѕроблему потребностей как двигател€ человеческого поведени€ . Ћевин разрешал с позиций гештальтпсихологии. ѕотребность означает дл€ . Ћевина некую динамическую зар€женную или напр€женную систему, образуемую взаимодействием сил в психологическом поле и стрем€щуюс€ к разр€дке. ¬ разр€дке этой напр€женности системы и состоит, по . Ћевину, удовлетворение потребности. ѕоэтому его теорию относ€т к гомеостатическим. ѕон€тие Ђпсихологическое полеї не означало дл€ него реального объективного окружени€. ќно выступало обозначением феноменального мира, который по существу есть отражение тех же напр€женных систем. –аскрытие структуры динамических напр€женных систем и их взаимоотношени€ с Ђпсихологическим полемї и должно, по мнению . Ћевина, €витьс€ объ€снением волевого действи€.
Ќесмотр€ на некоторую методологическую ограниченность учение . Ћевина сыграло положительную роль в истории психологии. ќн ввел в психологические исследовани€ новые параметры изучени€ человека: показал экспериментально, что в качестве предмета исследовани€ могут выступать потребности и мотивы человеческого поведени€. Ќо особенно велика роль . Ћевина и его школы в разработке экспериментальных приемов исследовани€ в области психологии личности. –аботы . Ћевина и его учеников (Ѕ. ¬. «ейгарник, “. ƒембо, ћ. ќвс€нкиной, ¬. ћалер, ј. арстен, ‘. ’оппе) позвол€ют эмпирически раскрывать отношени€, существующие между личностью и средой и внутри самой личности. “акими приемами стали методики, позвол€ющие исследовать уровень прит€заний, самооценку личности (феномены лучшего запоминани€ прерванных действий, пресыщени€ и т.д.).
. Ћевин считал, что уровень прит€заний формируетс€ в процессе конкретной де€тельности. ¬ формировании уровн€ прит€заний важнейшую роль играют самооценка и эмоционально переживаемый успех и неуспех достижени€ целей; уровень прит€заний €вл€етс€ важным образованием личности, с ним св€заны активность субъекта, уровень трудности выбираемых целей, сложна€ структура его аффективной жизни.
√руппа экспериментальных исследований в школе Ћевина была направлена на исследование возможности удержани€ и восстановлени€ побуждени€ к де€тельности. . Ћевин экспериментально показал, что любое действие, даже длительно и монотонно протекающее, возможно, если оно включено в систему потребностей человека (в пласт жизненных отношений).
ѕредлагаемые задани€ Ђ»сследование "уровн€ прит€заний"ї и Ђ»сследование процесса "пресыщени€"ї знаком€т с образцами методических приемов школы урта Ћевина, в которых Ц в отличие от эксперимента Ѕ. ¬. «ейгарник Ц наблюдаемые эффекты еще нельз€ назвать собственно экспериментальными, поскольку в такой же степени эти методики можно рассматривать и в качестве психодиагностических.
Ћитература: 23; 25, с. 276Ц283.
І 16. «адание 13. ћетодика Ђ”ровень прит€занийї
“ема задани€
«накомство с методической процедурой, позвол€ющей эксплицировать и анализировать динамику уровн€ прит€заний испытуемого в ситуации неопределенности.
¬ведение
»спытуемому предлагаетс€ р€д заданий (от 10 до 18), отличающихс€ по степени трудности. ¬се задани€ нанесены на карточки, которые расположены перед испытуемым в пор€дке возрастани€ их номеров. —тепень трудности задани€ соответствует величине пор€дкового номера карточки. ќднако результат его выполнени€ зависит также от экспериментатора*, который может создать ситуацию Ђуспехаї или Ђнеуспехаї, сославшись, например, на то, что Ђвышло врем€ї, фиксируемое им с помощью секундомера.
* “о есть эта методика предполагает некоторую игру с испытуемым (отсюда, в частности, сложилось представление об экспериментировании как Ђпсихологическом театреї) (ѕримеч. ред.).
»сследовани€, проведенные с помощью этой методики (‘. ’оппе, ћ. ёкнат, ћ. Ќеймарк, “. Ѕежанишвили, Ѕ. —еребр€кова, Ћ. Ѕороздина), показали, что, как правило, испытуемые выбирают после успешных решений задани€ более трудные и, наоборот, после р€да неудачных решений обращаютс€ к задани€м более легким. ”спешность выполнени€ первого задани€ вли€ет на выбор следующего, а его трудность свидетельствует о самооценке испытуемого.
ћетодика
ѕредлагаемые задани€ могут быть по своему содержанию весьма различными в зависимости от образовательного уровн€ и профессии испытуемых. Ќапример, школьникам или студентам технических вузов можно предлагать математические задачи, студентам гуманитарных факультетов Ц задачи, требующие знаний в области литературы, искусства; задани€ могут быть типа головоломок и т.д. »ными словами, содержание заданий должно соответствовать общеобразовательному уровню испытуемых. “олько при этом условии у них вырабатываетс€ серьезное отношение к ситуации эксперимента.
ƒл€ проведени€ опыта необходимо заготовить карточки размером в четверть листа, на которых четко обозначить цифры от 1 до 10 (это будет тыльна€ сторона, которую испытуемый видит при раскладе карточек на столе перед экспериментатором), и секундомер. ќбычно заготавливают два набора карточек, чтобы у испытуемого была возможность повторного выбора карточки одной и той же трудности (тогда идет двойна€ нумераци€: 1а и 1б, 2а и 2б и т.д.).
¬ данном опыте предлагаетс€ использовать в качестве экспериментального материала лабиринты. аждый лабиринт дан на лицевой стороне отдельной карточки. ¬ ѕриложении II даны 10 пар лабиринтов разной трудности.
ѕроцедура опыта. арточки раскладываютс€ в два р€да тыльной стороной. ѕосле предъ€влени€ инструкции испытуемому предлагаетс€ выбрать задачу Ц карточку с конкретным номером, обозначающим ее трудность. ѕосле выполнени€ очередной задачи экспериментатор предлагает каждый раз испытуемому: Ђ“еперь берите задачу какой хотите трудностиї. Ёкспериментатор фиксирует врем€ решени€ задачи и после каждой задачи говорит: ЂЁту задачу ¬ы выполнили в срок. —тавлю ¬ам плюсї или: Ђ¬ы не уложились во времени. —тавлю ¬ам минусї.
»нструкци€ испытуемому: Ђѕеред ¬ами лежат карточки, на обороте которых написаны задани€. Ќомера на карточках означают степень сложности заданий. «адани€ расположены по возрастающей сложности. Ќа решение каждой задачи отведено определенное врем€, которое ¬ам не известно. я слежу за ним с помощью секундомера. ≈сли не уложитесь в отведенное врем€, € буду считать, что задание не выполнено. «адани€ ¬ы должны выбирать самосто€тельної.
“аким образом, испытуемому даетс€ право самому выбирать сложность задани€. Ёкспериментатор же может по своему усмотрению увеличивать или уменьшать врем€, отведенное на выполнение задани€, тем самым произвольно вызыва€ у испытуемого переживание неудачи или удачи.
ѕосле того как опыт закончен, следует задать испытуемому вопрос: Ђ„ем ¬ы руководствовались при выборе задани€?ї






