ѕоказатель надежности Ц количественна€ характеристика одного или нескольких свойств, составл€ющих надежность объекта.
ѕоказатели надежности могут быть единичными и комплексными.
≈диничный показатель надежности характеризует одно из свойств, составл€ющих надежность объекта, а комплексный показатель Ц несколько свойств.
–азличают показатели безотказности, долговечности, ремонтопригодности и сохран€емости.
2.4.1. ѕоказатели безотказности
¬еро€тность безотказной работы Ц веро€тность того, что в пределах заданной наработки отказ объекта не возникнет.
≈сли в качестве наработки рассматриваетс€ врем€, то веро€тность безотказной работы
–(t) = ¬ер {T > t},
где –(t) Ц функци€ времени, представл€юща€ собой интегральный закон распределени€ времени безотказной работы объекта;
“ Ц случайное  врем€ безотказной работы от начала эксплуатации до первого отказа;
врем€ безотказной работы от начала эксплуатации до первого отказа;
t Ц врем€ эксплуатации.
ќчевидно, что 0 < P(t) <1. ¬еро€тность безотказной работы P(t) и веро€тность отказа Q(t) на интервале времени t образуют полную группу событий и св€заны соотношением P(t) + Q(t) =1 (рис. 2.3).

|
 
|

–ис. 2.3. «ависимости P(t) и Q(t)
¬еро€тность безотказной работы статистически определ€етс€ отношением числа однотипных объектов  , безотказно проработавших до момента времени t, к числу объектов N0 , работоспособных в начальный момент времени t = 0:
, безотказно проработавших до момента времени t, к числу объектов N0 , работоспособных в начальный момент времени t = 0:
 ,
,
где m Ц число объектов, отказавших за врем€ t.
ƒл€ режимов хранени€ и (или) транспортировани€ могут примен€тьс€ аналогично определ€емые показатели безотказности, например, веро€тность безотказного хранени€ (транспортировани€).
ƒл€ невосстанавливаемых объектов используют такие показатели как интенсивность отказов и средн€€ наработка до отказа.
»нтенсивность отказов Ц условна€ плотность веро€тности возникновени€ отказа невосстанавливаемого объекта, определ€ема€ дл€ рассматриваемого момента времени при условии, что до этого момента отказ не возник:
 (1/ч),
(1/ч),
где f(t) Ц плотность распределени€ наработки до отказа. Ётот показатель не св€зан с моментом начала работы объекта. —татистически  показывает, кака€ дол€ от работающих в некоторый момент времени t невосстанавливаемых объектов выходит из стро€ в единицу времени после этого момента:
показывает, кака€ дол€ от работающих в некоторый момент времени t невосстанавливаемых объектов выходит из стро€ в единицу времени после этого момента:
 ,
,
где  разность между числом отказов к моменту времени
разность между числом отказов к моменту времени  и числом отказов к моменту времени t.
и числом отказов к моменту времени t.
ƒл€ периода нормальной эксплуатации (рис.2.4) интенсивность отказов чаще всего €вл€етс€ величиной посто€нной, не завис€щей от времени, т.е.
 const.
const.
ƒл€ интервала приработки характерно снижение интенсивности отказов во времени ввиду быстрого вы€влени€ наименее надежных объектов. Ќа интервале нормальной эксплуатации интенсивность отказов стабилизируетс€.
»нтервал износа (старени€) показывает резкое увеличение количества отказов, что объ€сн€етс€ приближением объектов к предельному состо€нию.
—редн€€ наработка до отказа Ц математическое ожидание наработки объекта до первого отказа. ƒл€ интервала времени нормальной эксплуатации средн€€ наработка до отказа  . ¬ соответствии с этим дл€ интервала нормальной эксплуатации чаще всего характерен экспоненциальный закон распределени€ веро€тности безотказной работы
. ¬ соответствии с этим дл€ интервала нормальной эксплуатации чаще всего характерен экспоненциальный закон распределени€ веро€тности безотказной работы
|
|
|
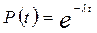 .
.


 –ис. 2.4. »зменение интенсивности отказов оборудовани€ во времени
–ис. 2.4. »зменение интенсивности отказов оборудовани€ во времени
ƒл€ восстанавливаемых объектов показател€ми безотказности €вл€ютс€ параметр потока отказов и средн€€ наработка на отказ.
ѕараметр потока отказов Ц отношение среднего числа отказов восстанавливаемого объекта за произвольно малую его наработку к значению этой наработки:
 ,
,
где  величина произвольно малой наработки;
величина произвольно малой наработки;
 среднее число отказов на интервале наработки
среднее число отказов на интервале наработки  .
.
ќтсюда также следует, что  плотность веро€тности возникновени€ отказа восстанавливаемого объекта, определ€ема€ дл€ рассматриваемого момента времени (математическое ожидание числа отказов в единицу времени, вз€тое дл€ рассматриваемого момента времени), т.е.
плотность веро€тности возникновени€ отказа восстанавливаемого объекта, определ€ема€ дл€ рассматриваемого момента времени (математическое ожидание числа отказов в единицу времени, вз€тое дл€ рассматриваемого момента времени), т.е.  ,
,
где P>1(t) - веро€тность того, что в течение времени  произойдет более одного отказа.
произойдет более одного отказа.
ѕон€тие потока отказов возникает в св€зи с тем, что дл€ восстанавливаемых объектов характерно чередование работоспособного состо€ни€ и восстановлени€ после отказа, т.е. процесс их эксплуатации можно представить чередованием интервалов времени работоспособного и неработоспособного состо€ни€.
Ќаиболее часто используетс€ (на основании обработки статистических данных) простейший поток, который характеризуетс€ следующими свойствами:
1) ординарностью, заключающейс€ в том, что веро€тность двух или более отказов в течение времени  стремитс€ к нулю при его уменьшении;
стремитс€ к нулю при его уменьшении;
2) стационарностью, заключающейс€ в том, что параметр потока отказов €вл€етс€ посто€нным, т.е.  const.
const.
3) отсутствием последствий, т.е. отказы, происшедшие ранее, не вли€ют на возникновение последующих отказов.
»з перечисленных свойств следует, что при простейшем потоке отказов

т.е. параметр потока отказов совпадает с интенсивностью отказов объекта. ¬ этом случае справедливо соотношение  .
.
—редн€€ наработка на отказ Ц отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. ƒругими словами, если наработка представл€ет собой врем€, то это математическое ожидание времени между двум€ соседними отказами. ¬ общем случае величина средней наработки на отказ зависит от длительности интервала, в течение которого она определ€етс€. Ёто обусловлено непосто€нством характеристики потока отказов.
—огласно определению средн€€ наработка на отказ

где  математические ожидани€ числа отказов за наработки t2,t1 соответственно, (t2>t1).
математические ожидани€ числа отказов за наработки t2,t1 соответственно, (t2>t1).
ƒл€ интервала нормальной работы при экспоненциальном законе распределени€ отказов справедливо
 .
.
ѕоказатель T0 может быть определен на основании статистических данных:
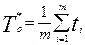 ,
,
где  Ц врем€ безотказной работы между (i Ц 1)-м и i- м отказами;
Ц врем€ безотказной работы между (i Ц 1)-м и i- м отказами;
m Ц общее число отказов.
2.4.2. ѕоказатели долговечности
—редний ресурс - математическое ожидание ресурса. Ётот термин, а также все последующие термины требуют указани€ вида действий после наступлени€ предельного состо€ни€. ѕоэтому средний ресурс может быть:
а) средним ресурсом до среднего ремонта объекта;
б) средним ресурсом до капитального ремонта объекта;
в) средним ресурсом до сн€ти€ объекта с эксплуатации (полным средним ресурсом).
—редний ресурс на основе статистических данных определ€етс€ так:
 ,
,
где tрi Ц ресурс i -го объекта (оборудовани€, транспортного средства);
|
|
|
N Ц количество рассматриваемых объектов.
√амма-процентный ресурс Ц наработка, в течение которой объект не достигнет предельного состо€ни€ с заданной веро€тностью  , выраженной в процентах.
, выраженной в процентах.
√амма-процентный ресурс может быть гамма-процентным ресурсом до среднего ремонта, капитального ремонта, до сн€ти€ объекта с эксплуатации (полный гамма-процентный ресурс).
Ќазначенный ресурс Ц суммарна€ наработка объектов, при достижении которой применение по назначению должно быть прекращено. »з этого определени€ следует, что эксплуатаци€ объекта по истечении назначенного ресурса прекращаетс€, независимо от его состо€ни€.
Ќазначенный ресурс может быть до среднего, капитального ремонта или полным (т.е. до сн€ти€ и списани€ объекта с эксплуатации).
—редний срок службы Ц математическоеожидание срока службы. —рок службы Ц календарна€ продолжительность эксплуатации объекта от начала эксплуатации или еЄ возобновлени€ после среднего или капитального ремонта до предельного состо€ни€.
—татистически средний срок службы определ€етс€ по формуле:
 ,
,
где tсл.i Ц срок службы i Цго объекта;
N Ц число рассматриваемых объектов.
—редний срок службы может быть до среднего, капитального ремонта или полный средний срок службы.
√амма-процентный срок службы Ц календарна€ продолжительность от начала эксплуатации объекта, в течение которой он не достигнет предельного состо€ни€ с заданной веро€тностью  , выраженной в процентах. √амма-процентный срок службы может быть до среднего, капитального ремонта или полный гамма-процентный срок службы (т.е. до списани€ объекта).
, выраженной в процентах. √амма-процентный срок службы может быть до среднего, капитального ремонта или полный гамма-процентный срок службы (т.е. до списани€ объекта).
ћогут также использоватьс€ показатели долговечности в виде средних (гамма-процентных) ресурсов или сроков службы между средними ремонтами, между капитальными ремонтами, от последнего капитального ремонта до списани€ объекта.
Ќазначенный срок службы Ц календарна€ продолжительность от начала эксплуатации объекта, при достижении которой применение по назначению должно быть прекращено. Ќазначенный срок службы может быть до среднего ремонта, капитального ремонта и полный назначенный срок службы (т.е. до списани€ объекта).
2.4.3. ѕоказатели ремонтопригодности
¬еро€тность восстановлени€ работоспособного состо€ни€ - веро€тность того, что врем€ восстановлени€ работоспособного состо€ни€ не превысит
заданного, т.е.
 ,
,
где t¬ Ц фактическа€ продолжительность работ по восстановлению работоспособного состо€ни€ объекта;
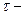 заданна€ (допустима€) продолжительность работ по восстановлению работоспособного состо€ни€ объекта.
заданна€ (допустима€) продолжительность работ по восстановлению работоспособного состо€ни€ объекта.
ѕри практических расчетах наиболее часто примен€етс€ экспоненциальный закон распределени€ восстановлени€, дл€ которого справедливо соотношение
 ,
,
где  интенсивность восстановлени€;
интенсивность восстановлени€; 
T¬ Ц среднее врем€ восстановлени€.
—реднее врем€ восстановлени€ Ц математическое ожидание времени восстановлени€ работоспособного состо€ни€.
—татистическое значение среднего времени восстановлени€ работоспособности определ€етс€ следующим образом:
 ,
,
где tвi Ц врем€, затрачиваемое на восстановление работоспособности по причине отказа; m Ц число отказов.
—ледует отметить некоторую сложность оценивани€ ремонтопригодности объектов рассмотренными показател€ми. Ёто объ€сн€етс€ тем, что показатели  , T¬ завис€т не только от свойств объекта, но и от системы восстановлени€: средств и методов восстановлени€, организации работ по восстановлению, квалификации специалистов по ремонту и техническому обслуживанию.
, T¬ завис€т не только от свойств объекта, но и от системы восстановлени€: средств и методов восстановлени€, организации работ по восстановлению, квалификации специалистов по ремонту и техническому обслуживанию.
2.4.4. ѕоказатели сохран€емости
—редний срок сохран€емости Ц математическое ожидание срока сохран€емости. (ѕон€тие Усохран€емостьФ уже было рассмотрено.)
√амма-процентный срок сохран€емости Ц срок сохран€емости, достигаемый объектом с заданной веро€тностью  , выраженной в процентах.
, выраженной в процентах.
2.4.5. омплексные показатели надежности
таким показател€м, отражающим несколько свойств объекта, относ€тс€ в первую очередь показатели готовности.
оэффициент готовности Ц веро€тность того, что объект окажетс€ в работоспособном состо€нии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объектов по назначению не предусматриваетс€. Ётот показатель учитывает как показатель безотказности “, так и показатель ремонтопригодности T¬:
|
|
|
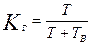 .
.
Ёта формула справедлива, если предусматриваетс€ немедленное начало восстановлени€ отказавшего объекта. оэффициент готовности не учитывает врем€, которое затрачивают на техническое обслуживание. ќднако это врем€ вли€ет на готовность объекта к выполнению основных функций при его использовании по назначению. ѕоэтому кроме коэффициента готовности используют более общий показатель Ц коэффициент технического использовани€.
оэффициент технического использовани€ Ц отношение математического ожидани€ интервалов времени пребывани€ объектов в работоспособном состо€нии за некоторый период эксплуатации к сумме математических ожиданий интервалов времени пребывани€ объекта в работоспособном состо€нии, простоев, обусловленных техническим обслуживанием и ремонтом за тот же период эксплуатации:
 ,
,
где  математические ожидани€ времени пребывани€ объекта в работоспособном состо€нии, суммарного времени простоев из-за технических обслуживаний, суммарного времени, затрачиваемого на ремонты, соответственно.
математические ожидани€ времени пребывани€ объекта в работоспособном состо€нии, суммарного времени простоев из-за технических обслуживаний, суммарного времени, затрачиваемого на ремонты, соответственно.
ƒл€ некоторых объектов характерно длительное ожидание использовани€ по назначению (например, резервное оборудование транспортных средств). ¬ режиме ожидани€ возможны отказы, поэтому возникает необходимость его восстановлени€. ƒл€ подобных объектов используют такой показатель как коэффициент оперативной готовности.
оэффициент оперативной готовности Ц веро€тность того, что объект окажетс€ в работоспособном состо€нии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматриваетс€, и начина€ с этого момента будет работать безотказно в течение заданного интервала времени:
K ог = K гож P(tр),
где K гож Ц коэффициент готовности объекта в режиме ожидани€;
K гож = T ож / (T ож + T в);
T ож Ц среднее врем€ между отказами в режиме ожидани€;
P(tр) Ц веро€тность безотказной работы объекта в течение заданного времени tр (в рабочем режиме).
оэффициент планируемого применени€ Ц дол€ периода эксплуатации, в течение которой объект не должен находитьс€ на плановом техническом обслуживании и ремонте:
 .
.
„ем безотказнее объект, чем выше его приспособленность к техническому обслуживанию и ремонту и чем совершеннее система технического обслуживани€ и ремонта, тем выше  .
.
«десь: tэ Ц продолжительность эксплуатации объекта;
 Ц суммарные продолжительности планируемых технических обслуживаний и ремонтов объекта.
Ц суммарные продолжительности планируемых технических обслуживаний и ремонтов объекта.
оэффициент сохран€емости эффективности Ц отношение значени€ показател€ эффективности за определенную продолжительность эксплуатации к номинальному значению этого показател€, вычисленному при условии, что отказы объекта в течение того же периода эксплуатации не возникают:
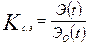 ,
,
где  Ц показатель эффективности объекта, эксплуатируемого в период времени t;
Ц показатель эффективности объекта, эксплуатируемого в период времени t;
 Ц то же, но при условии, что отказы за врем€ t отсутствуют.
Ц то же, но при условии, что отказы за врем€ t отсутствуют.






