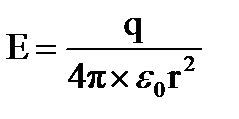| dS |
| n |
‘=∫AndS.
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAHFv/wcUA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWsCMRSE7wX/Q3iCt5qtoJXVKKKIWuihtnp+bJ6b pZuXJYnu6q9vCoUeh5n5hpkvO1uLG/lQOVbwMsxAEBdOV1wq+PrcPk9BhIissXZMCu4UYLnoPc0x 167lD7odYykShEOOCkyMTS5lKAxZDEPXECfv4rzFmKQvpfbYJrit5SjLJtJixWnBYENrQ8X38WoV SOtX5vo4vE7Pj3a3xvPp/W1zUmrQ71YzEJG6+B/+a++1gsl4BL9n0hGQix8AAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQAcW//BxQAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA " filled="f" strokecolor="black [3213]" strokeweight="1pt"> ¬ упрощенном выводе теоремы √аусса источником пол€ €вл€етс€ точечный зар€д q, а поверхность интегрировани€ S- сфера радиусом r, концентрична€ данному зар€ду. ќказываетс€, что полученный при этом результат справедлив в общем случае - дл€ любой замкнутой поверхности произвольной формы и произвольной системы зар€дов.
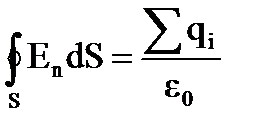 ‘ќ–ћ”Ћ»–ќ¬ ј “≈ќ–≈ћџ √ј”——ј: ѕоток вектора электростатической индукции через замкнутую поверхность S равен алгебраической сумме зар€дов, заключенных внутри поверхности интегрировани€, деленной на e0
‘ќ–ћ”Ћ»–ќ¬ ј “≈ќ–≈ћџ √ј”——ј: ѕоток вектора электростатической индукции через замкнутую поверхность S равен алгебраической сумме зар€дов, заключенных внутри поверхности интегрировани€, деленной на e0
ѕ–»ћ≈Ќ≈Ќ»≈ “≈ќ–≈ћџ √ј”——ј ƒЋя –≈Ў≈Ќ»я ќ—Ќќ¬Ќќ… «јƒј„» ЁЋ≈ “–ќ—“ј“» »- по заданному распределению зар€дов определить напр€женность электростатического пол€ в заданной точке пространства. »спользование теоремы √аусса дл€ определени€ напр€женности электростатического пол€ имеет смысл только при определенных услови€х, налагаемых на поверхность интегрировани€: либо силовые линии пол€ направлены параллельно поверхности интегрировани€ и тогда поток вектора ≈ через такую поверхность равен нулю, либо силовые линии пол€ направлены параллельно поверхности интегрировани€ и тогда поток вектора ≈ через такую поверхность равен нулю.