You throw a ball vertically upward from the roof of a tall building. The ball leaves your hand at a point even with the roof railing with an upward speed of 15 m/s; the ball is then in free fall. On its
way back down, it just misses the railing. Find (a) the ball’s position and velocity 1.00 s and 4.00 s after leaving your hand; (b) the ball’s velocity when it is 5.00 m above the railing; (c) the maximum
height reached; (d) the ball’s acceleration when it is at its maximum height.
6. A car travels in the _ x -direction on a straight and level road. For the first 4.00 s of its motion, the average velocity of the car is 6.25 m/s. How far does the car travel in 4.00 s?
7. Starting from the front door of your ranch house, you walk 60.0 m due east to your windmill, and then you turn around and slowly walk 40.0 m west to a bench where you sit and watch the sunrise. It takes you 28.0 s to walk from your house to the windmill and then 36.0 s to walk from the windmill to the bench. For the entire trip from your front door to the bench, what are (a) your average velocity and (b) your average speed?
8. A bird is flying due east. Its distance from a tall building is given by x(t) = 28.0 m + (12.4 m/s)t – (0.045 m/s3)t3. What is the instantaneous velocity of the bird when t = 8.0 s?
9. A car’s velocity as a function of time is given by ʋx (t) = 
2, where 
and 
3. Calculate the instantaneous acceleration for t = 0 and t = 5.0 s. (c)
10. An antelope moving with constant acceleration covers the distance between two points 70.0 m apart in 7.00 s. Its speed as it passes the second point is 15 m/s. (a) What is its speed at the first point? (b) What is its acceleration?
11. (a) If a flea can jump straight up to a height of 0.440 m, what is its initial speed as it leaves the ground? (b) How long is it in the air?
12. A juggler throws a bowling pin straight up with an initial speed of 8.20 m s. How much time elapses until the bowling pin returns to the juggler’s hand?
13. A brick is dropped (zero initial speed) from the roof of a building. The brick strikes the ground in 2.50 s. You may ignore air resistance, so the brick is in free fall. (a) How tall, in meters, is the
building? (b) What is the magnitude of the brick’s velocity just before it reaches the ground?
Dynamics
Superposition of forces
| Three professional wrestlers are fighting over a champion’s belt. Figure 4.8a shows the horizontal force each wrestler applies to the belt, as viewed from above. The forces have magnitudes F1 = 250 N, F2 = 50 N and F3 = 120 N. Find the x - and y -components of the net force on the belt, and find its magnitude and direction | 
|
Mass and weight
A 2.49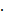 
104 N Rolls-Royce Phantom traveling in the x-direction makes an emergency stop; the x -component of the net force acting on it is – 1.83 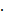104 N. What is its acceleration?
3. A 68.5-kg skater moving initially at 240 m/s on rough horizontal ice comes to rest uniformly in 3.52 s due to friction from the ice. What force does friction exert on the skater?
4. A crate with mass 32.5 kg initially at rest on a warehouse floor is acted on by a net horizontal force of 140 N. (a) What acceleration is produced? (b) How far does the crate travel in 10.0 s? (c) What is its speed at the end of 10.0 s?
5. An astronaut’s pack weighs 17.5 N when she is on earth but only 3.24 N when she is at the surface of an asteroid. (a) What is the acceleration due to gravity on this asteroid? (b) What is the mass of the pack on the asteroid?
Gravity on Mars
A robotic lander with an earth weight of 3430 N is sent to Mars, which has radius R = 3.6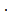 
106 m and mass m = 6.42 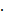1023 rg. Find the weight of the lander on the Martian surface and the acceleration there due to gravity, gM.
7. The mass of Venus is 81.5% that of the earth, and its radius is 94.9% that of the earth. (a) Compute the acceleration due to gravity on the surface of Venus from these data. (b) If a rock weighs 75.0 N on earth, what would it weigh at the surface of Venus?
8. Rhea, one of Saturn’s moons, has a radius of 765 km and an acceleration due to gravity of 0.278 m/s2 at its surface. Calculate its mass and average density.
Tensile stress and strain
A steel rod 2.0 m long has a cross-sectional area of 0.3 cm2. It is hung by one end from a support, and a 550-kg milling machine is hung from its other end. Determine the stress on the rod and the resulting strain and elongation.
10. A circular steel wire 2.00 m long must stretch no more than 0.25 cm when a tensile force of 400 N is applied to each end of the wire. What minimum diameter is required for the wire?
11. A metal rod that is 4.00 m long and in crosssectional area is found to stretch 0.20 cm under a tension of 5000 N. What is Young’s modulus for this metal?
