„асовими характеристиками под≥й Ч вершин с≥тьового граф≥≠ка Ч Ї ранн≥ та п≥зн≥ терм≥ни настанн€ в≥дпов≥дних под≥й, пов'€заних ≥з виконанн€м проекту, та резерви часу цих под≥й.
–анн≥й терм≥н настанн€ под≥њ - це такий момент часу, коли буде завершено ус≥ роботи, що обумовлюють цю под≥ю. –анн≥ те≠рм≥ни настанн€ под≥й обчислюютьс€ рекурентно за формулами:
 (10.1)
(10.1)
де n Ц загальна к≥льк≥сть вершин с≥тьового граф≥ка;
U - множина його дуг;
(i, j) 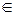 U Ц позначенн€ такоњ дуги, €ка виходить з вершин ≥ та входить у j-ту вершину графа;
U Ц позначенн€ такоњ дуги, €ка виходить з вершин ≥ та входить у j-ту вершину графа;
t(i, j) Ц тривал≥сть виконанн€ роботи i →j:
≈(≥) Ц ранн≥й терм≥н настанн€ ≥-оњ под≥њ, в≥дпов≥дно;
≈(j) Ц ранн≥й терм≥н настанн€ j-оњ под≥њ (i, j= 1,2,Е,n).
“ривал≥сть виконанн€ комплексу роб≥т “* дор≥внюЇ ранньому терм≥ну настанн€ його к≥нцевоњ под≥њ. “аким чином,
“* = ≈(n) (10.2)
ѕ≥зн≥й терм≥н настанн€ под≥њ Ч де момент часу, переви≠щенн€ €кого при настанн≥ ц≥Їњ под≥њ призведе-до затримки з вико≠нанн€м проекту у ц≥лому. ѕ≥зн≥ терм≥ни настанн€ под≥й обчис≠люютьс€ рекурентно за формулами:
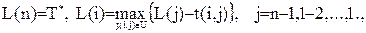 (10.3)
(10.3)
 (10.4)
(10.4)
ѕод≥њ, €к≥ не допускають ан≥€коњ затримки з њх настанн€м, називаютьс€ ктиричними. ƒл€ кожноњ критичноњ точки њњ резерв часу дор≥внюЇ нулю:
R(j*)= 0, €кщо j* - критична под≥€. (10.5)
ѕриклад 10.2 ќбчислимо числов≥ характеристики под≥й та тривал≥сть виконанн€ проекту, с≥тьковий граф≥к €кого було наведено на рис.10.11.
–анн≥ терм≥ни настанн€ под≥й розшукуютьс€ за с≥тьковим граф≥ком методом обчислень у пр€мому пор€дку Ц в≥д початковоњ до к≥нцевоњ под≥њ:
≈(1) = 0.
≈(2) = ≈(1) +t(1, 2) = 0+12,
E(3) = max { E(1) + t (1,3);E(2) + t(2,3)}= max {0+20;12+0} = 20,
E(4) = max { E(1) + t (1,4);E(2) + t(2,4)}= max {0+27;12+0} = 27,
E(5) = E(3) + t (3,5) = 20+7 = 27,
E(6) = E(4) + t (4,6) = 27+14 = 41,
E(7) = max { E(5) + t (5,7);E(6) + t(6,7)}= max {27+13; 41+0} = 41,
E(8) = max { E(6) + t (6,8);E(7) + t(7,8)}= max {41 + 11; 41 + 15} = 56.
“ривал≥сть виконанн€ комплексу роб≥т сп≥впадаЇ з ранн≥м терм≥ном настанн€ останньоњ Ц восьмоњ Ц под≥њ. ќтже,
“* = 56
ѕ≥зн≥ терм≥ни настанн€ под≥й розшукуютьс€ за с≥тьковим граф≥ком методом обчислень у зворотному пор€дку в≥д к≥нцевоњ до початковоњ под≥њ:
L(8) = “* = 56,
L(7) = L(8)- t (7,8) = 56 Ц 15 = 41,
L(6) = min {L(8) + t (6,8); L(7) - t(6,7)}= min {56-11; 41-0} = 41,
L(5) = L(7) Ц t(5,7) = 41 Ц 13 = 28,
L(4) = L(6) Ц t(4,6) = 41 Ц 14 = 27,
L(3) = L(5) Ц t(3,5) = 28 Ц 7 = 21,
L(2) = min {L(4) + t (2,4); L(3) - t(2,3)}= min {27-0; 21-0} = 21,
L(1) = min {L(4) + t (1,4); L(3) - t(1,3); L(2) - t(1,2)}= min {27-0; 21Ч20; 21-12} = 0.
ѕокажемо терм≥ни настанн€ под≥й на с≥тьовому граф≥ку (рис. 10.12). Ќа цьому рисунку також вид≥лено вершини, €к≥ в≥д≠пов≥дають критичним под≥€м (дл€ таких под≥й ранн≥й терм≥н на≠станн€ ≈ сп≥впадаЇ з њх п≥зн≥м терм≥ном настанн€ L).

–ис. 10.12
Ќа рис. 10.12. дл€ кожного комплексу роб≥т надано ранн≥й (≈) та п≥зн≥ (L)терм≥ни настанн€ под≥й  (критичн≥ под≥њ 1, 4, 6, 7 та 8 вид≥лено).
(критичн≥ под≥њ 1, 4, 6, 7 та 8 вид≥лено).
–анн≥ та п≥зн≥ терм≥ни настанн€ под≥й, а також њхн≥ резерви часу наведен≥ у табл. 10.3
|
|
|
“абл. 10.3

ѕ≥сл€ обчисленн€ часових характеристик под≥й визначають часов≥ характеристики кожноњ з роб≥т проекту.
«а аналог≥Їю до под≥й ус≥ роботи проекту також розпод≥л€≠ютьс€ на критичн≥ та некритичн≥. ритичн≥ роботи не мають ре≠зерву часу на њх виконанн€. Ќавпаки, некритичн≥ роботи мають певний резерв часу, тобто де€ке зап≥зненн€ з њх завершенн€м не призводитиме до затримки ≥з виконанн€м проекту в ц≥лому. —е≠ред часових характеристик роб≥т розр≥зн€ють повний, в≥льний та незалежний резерви. ”с≥ ц≥ резерви часу обчислюютьс€ на основ≥ даних про ранн≥ та п≥зн≥ терм≥ни настанн€ в≥дпов≥дних под≥й.
ѕовний резерв часу ћ (≥, j) роботи (≥, j) Ч це максимально можлива затримка у виконанн≥ ц≥Їњ роботи, €ка не призведе до за≠тримки ≥з виконанн€м усього проекту за умов, що тривал≥сть ≥н≠ших роб≥т не зм≥нюватиметьс€:
 M(I,j)=L(j)-E(i)-t(i,j) (10.6)
M(I,j)=L(j)-E(i)-t(i,j) (10.6)
де: L(j) Ц п≥зн≥й терм≥н настанн€ j-оњ под≥њ, €ка Ї к≥нцевою дл€ роботи (i, j);
≈ (≥) Ц ранн≥й терм≥н настанн€ ≥-оњ под≥њ, €ка Ї вих≥дною дл€ ц≥Їњ роботи;
t (i, j) - нормативна тривал≥сть виконанн€ в≥дпов≥дноњ роботи.
ƒл€ кожноњ критичноњ роботи њњ повний резерв часу дор≥в≠нюЇ нулю:
 дл€ вс≥х
дл€ вс≥х  (10.7)
(10.7)
де U * Ч множина ус≥х критичних роб≥т проекту.
Ўл€х в≥д початковоњ вершини до к≥нцевоњ, €кий складаЇтьс€ лише ≥з критичних роб≥т, називаЇтьс€ критичним шл€хом с≥≠тьового граф≥ка. ƒовжина критичного шл€ху зб≥гаЇтьс€ ≥з трива≠л≥стю виконанн€ усього комплексу роб≥т “*.
ѕрим≥тка. —≥тьовий граф≥к може мати дек≥лька р≥зних крити≠чних шл€х≥в. ƒовжина кожного з них також дор≥внюЇ тривалост≥ виконанн€ усього проекту.
¬≥льний резерв часу N(i, j) роботи (≥, j) Ч це така максималь≠но можлива затримка ≥з виконанн€м ц≥Їњ роботи, €ка не впливаЇ на терм≥ни виконанн€ ус≥х наступних роб≥т:
N(i,j) = E(J)-E(i)-t(iJ). (10.8)
Ќезалежний резерв часу –{≥, j) роботи (≥, j) характеризуЇ таку максимально можливу затримку ≥з виконанн€м ц≥Їњ роботи, €ка не впливаЇ на терм≥ни виконанн€ ус≥х ≥нших роб≥т проекту:
–(≥, j) = max {0; E(j) Ц L(i) - t(i, j)}. (10.9)
ƒл€ кожноњ з роб≥т ус≥ три види резерв≥в часу задовольн€ють нер≥вн≥сть:
ћ{≥, j)  N(i, j)
N(i, j)  –(≥, j)
–(≥, j)  0. (10.10)
0. (10.10)
ѕриклад 10.3. «ведемо разом ус≥ часов≥ характеристики роб≥т (дуг) с≥тьового граф≥ка, наведеного на рис. 10.13. “акими характе≠ристиками роботи (/, j) Ї:
Х тривал≥сть Ч t(i, j);
Х ранн≥й терм≥н початку Ч ран≥ше €кого розпочати роботу
неможливо Ч ≈(њ);
Х п≥зн≥й терм≥н зак≥нченн€ Ч перевищенн€ €кого призведе до
затримки ≥з завершенн€м проекту в ц≥лому Ч L(j);
Х ус≥ резерви часу Ч ћ(≥, j), N(i, j) та –(≥, j), €к≥ розраховують≠с€ за формулами (10.6), (10.8), (10.9).
дл€ роботи (3, 5) маЇмо:
t<(3,5) = 7;E(3) = 20;L(5) = 28;
ћ(3, 5) = 28 - 20 - 7 = 1; N (3, 5) = 27 - 20 - 7 = 0;
–(3, 5) = max {0; 27-21-7} = 0.
–езерви часу ус≥х дуг с≥тьового граф≥ка та критичний шл€х  показано на рис. 10.13. „асов≥ характеристики ус≥х роб≥т проекту, що розгл€даЇтьс€, наведено у табл. 10.4.
показано на рис. 10.13. „асов≥ характеристики ус≥х роб≥т проекту, що розгл€даЇтьс€, наведено у табл. 10.4.
Ќа с≥тьовому граф≥ку комплексу роб≥т застосовано позначен≠н€: ранн≥й та п≥зн≥й терм≥ни настанн€ под≥й  ;
;
резерви часу роб≥т: V, N, P, де ћ - повний резерв; N - в≥льний; – - незалежний; роботи критичного шл€ху (1Ч4; 4Ч6; 6Ч7; 7Ч8) вид≥лено.
.
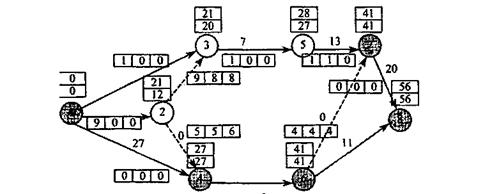
–ис. 10.13
“абл. 10.4

«авершений с≥тьовий граф≥к (рис. 10.13) ≥ таблиц≥ про часов≥ характеристики под≥й та роб≥т (табл. 10.2 ≥ 10.3) Ї зручними ≥нстру≠ментами при обговоренн≥ та затвердженн≥ календарного плану ≥ подальшому контрол≥ за виконанн€м проекту.
|
|
|
10.3 —≥тьове плануванн€ з урахуванн€м вартост≥ виконанн€ роб≥т
“ривал≥сть виконанн€ окремих роб≥т може бути скорочена за рахунок залученн€ додаткових ф≥нансових ресурс≥в. ” таких ви≠падках залежн≥сть вартост≥ виконанн€ проекту в≥д терм≥ну його виконанн€ Ї спадною: б≥льш≥й тривалост≥ виконанн€ проекту в≥д≠пов≥дають менш≥ витрати, ≥ навпаки Ч менш≥й тривалост≥ вико≠нанн€ проекту в≥дпов≥дають б≥льш≥ витрати.
јле при затримц≥ ≥з зак≥нченн€м проекту можуть мати м≥сце додатков≥ збитки, пов'€зан≥ ≥з штрафами за порушенн€ умов кон≠тракту на виконанн€ проекту. “обто залежн≥сть втрат, пов'€заних ≥з зап≥зненн€м завершенн€ проекту, Ї зростаючою в≥д тривалост≥ строку виконанн€ проекту.
ѕостаЇ проблема визначенн€ такоњ стратег≥њ виконанн€ проек≠ту, при €к≥й загальн≥ витрати, що пов'€зан≥ ≥з виконанн€м проекту ≥ з втратами внасл≥док затримки ≥з його завершенн€м, будуть м≥≠н≥мальними (рис. 10.14).

–ис. 10.14
ќпрацюЇмо спочатку питанн€ про оптим≥зац≥ю с≥тьового гра≠ф≥ка за показником вартост≥ виконанн€ проекту дл€ випадку, ко≠ли задано директивний терм≥н завершенн€ всього комплексу ро≠б≥т Td.
Ќехай {1, 2,..., п) Ч множина вершин с≥тьового граф≥ка, U Ч множина його дуг. ѕрипустимо, що тривал≥сть tlt роботи (i,j Ї и) може зм≥нюватись у певних межах часу, де Djj Ч тривал≥сть виконанн€ ц≥Їњ роботи, скаж≥мо, у в≥д dtj до Dtj одиниць нормативно≠му режим≥, a dy Ч тривал≥сть њњ виконанн€ у максимально при≠скореному режим≥.
Ќехай ctj Ч варт≥сть виконанн€ роботи (i,j) у нормальному режим≥, а —ij + ΔCij Ч витрати на њњ виконанн€ у максимально прискореному режим≥. ѕрипустимо, що залежн≥сть вартост≥ zij в≥д тривалост≥ виконанн€ tij Ї л≥н≥йною:
 (10.11)
(10.11)
ўо ≥люструЇ рисунок 10.15

–ис. 10.15
“од≥ задача оптим≥зац≥њ с≥тьового граф≥ка за показником м≥н≥м≥зац≥њ загальноњ вартост≥ z виконанн€ проекту, з урахуванн€м вимоги завершенн€ проекту у заданий директивний терм≥н Td, набираЇ вигл€ду:
«найти tij, zij, Ti, Tj, i,j =  , що належать област≥ G, ви≠значеноњ умовами:
, що належать област≥ G, ви≠значеноњ умовами:
 (10.12)
(10.12)
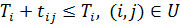 (10.13)
(10.13)
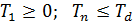 (10.14)
(10.14)
≥ м≥н≥м≥з≥рують функц≥ю ц≥л≥:

«адача (10.12)Ч(10.15) Ї задачею л≥н≥йного програмуванн€ з двосторонн≥ми обмеженн€ми на ttj. якщо њњ розв'€зок ≥снуЇ, тоб≠то коли Ї можлив≥сть виконати проект за директивний терм≥н Td, результатом розв'€зуванн€ задач≥ будуть так≥ тривалост≥ вико≠нанн€ кожноњ з роб≥т tij*, (≥,j) Ї U, за €ких варт≥сть виконанн€ z* всього проекту буде найменшою.
” загальному випадку задачу оптим≥зац≥њ с≥тьового граф≥ка з урахуванн€м часу та вартост≥ можна розгл€дати €к двоц≥льову
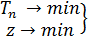 , (10.16)
, (10.16)
в €к≥й перша ц≥льова функц≥€ ор≥ЇнтуЇ на най скор≥ше вико≠нанн€ проекту (терм≥ну настанн€ к≥нцевоњ под≥њ), а другаЧ на м≥н≥м≥зац≥ю витрат, пов'€заних ≥з виконанн€м проекту. ќбме≠женн€ (10.12)Ч(10.14) визначають множину допустимих план≥в.
“аким чином, задачу (10.12)Ч(10.15) сл≥д розгл€дати лише €к спрощений п≥дх≥д до розв'€занн€ ц≥льовоњ проблеми оптим≥зац≥њ с≥тьового граф≥ка. Ќаступним кроком зд≥йсненн€ ц≥льовоњ опти≠м≥зац≥њ буде досл≥дженн€ задач≥ (10.12)Ч(10.15) €к параметричноњ в≥дносно директивного терм≥ну виконанн€ проекту Td. ÷е дозво≠лить визначити залежн≥сть оптимальноњ вартост≥ z* в≥д Td (рис. 10.16), що Ї корисним дл€ узгодженн€ терм≥н≥в виконанн€ проекту та необх≥дних дл€ цього витрат.

–ис. 10.16
ѕриклад 10.4 –озгл€немо проект, с≥тьова модель €кого наведена на рис.10.17, а показники тривалост≥ та вартост≥ кожного ≥з роб≥т надан≥ у табл. 10.5.

“абл. 10.5

Ќеобх≥дно визначити тривал≥сть та варт≥сть виконанн€ проек≠ту за умов:
Чтривал≥сть кожноњ ≥з роб≥т буде максимальною;
Чтривал≥сть кожноњ роботи буде м≥н≥мальною.
ѕобудувати граф≥к залежност≥ оптимальноњ вартост≥ виконан≠н€ проекту в≥д директивноњ тривалост≥ його виконанн€ Td.
|
|
|
–озв'€зуванн€. 1. ѕобудуЇмо с≥тьовий граф≥к проекту, обра≠вши за тривалост≥ роб≥т максимально можлив≥ терм≥ни њх вико≠нанн€. ќбчислимо також часов≥ характеристики L, ≈ ус≥х под≥й та повн≥ резерви часу ћ ус≥х роб≥т под≥й проекту (рис. 10.18).

–ис. 10.18
“аким чином, максимальна тривал≥сть виконанн€ проекту “max = 9 (м≥с€ц≥в). ќск≥льки кожна з роб≥т виконуватиметьс€ з м≥н≥мальною варт≥стю, робимо висновок, що оптимальна варт≥сть проекту при Td > 9 дор≥внюватиме 6 + 12 + 5 = 23 (тис. грн).
2. ѕроанал≥зуЇмо тепер проект за умов, коли тривал≥сть вико≠нанн€ кожноњ з роб≥т буде м≥н≥мальною (рис. 10.19).

–ис.10.19
ћ≥н≥мальна тривал≥сть виконанн€ проекту 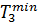 = 6 м≥сц≥в. ѕроте оптимальна варт≥сть виконанн€ проекту за 6 м≥с€ц≥в не дор≥внюва≠тиме сум≥ максимальних вартостей виконанн€ кожноњ ≥з роб≥т 10 + + 15 + 8 = 33 (тис. грн). ÷е по€снюЇтьс€ тим, що робота (1, 3) не Ї критичною та маЇ резерв часу ћ{1, 3) = 1 м≥с. ќтже, €кщо цю ро≠боту виконати не за 5, а за 6 м≥с, тривал≥сть виконанн€ проекту не зб≥льшитьс€. јле зменшитьс€ варт≥сть виконанн€ роботи (1, 3) оск≥льки z13 (5 м≥с.) = 15 тис. грн (табл. 10,5), a z13 (6 м≥с.) = = 12 +
= 6 м≥сц≥в. ѕроте оптимальна варт≥сть виконанн€ проекту за 6 м≥с€ц≥в не дор≥внюва≠тиме сум≥ максимальних вартостей виконанн€ кожноњ ≥з роб≥т 10 + + 15 + 8 = 33 (тис. грн). ÷е по€снюЇтьс€ тим, що робота (1, 3) не Ї критичною та маЇ резерв часу ћ{1, 3) = 1 м≥с. ќтже, €кщо цю ро≠боту виконати не за 5, а за 6 м≥с, тривал≥сть виконанн€ проекту не зб≥льшитьс€. јле зменшитьс€ варт≥сть виконанн€ роботи (1, 3) оск≥льки z13 (5 м≥с.) = 15 тис. грн (табл. 10,5), a z13 (6 м≥с.) = = 12 +  (15-12) = 14 (тис. грн) (формула (10.11) та вих≥дн≥ дан≥ з табл. 10.11, тобто оптимальна варт≥сть виконанн€ проекту за 6 м≥с. дор≥внюватиме 10 + 14 + + 8 = 32 (тис. грн).
(15-12) = 14 (тис. грн) (формула (10.11) та вих≥дн≥ дан≥ з табл. 10.11, тобто оптимальна варт≥сть виконанн€ проекту за 6 м≥с. дор≥внюватиме 10 + 14 + + 8 = 32 (тис. грн).
3. ўоб побудувати граф≥к залежност≥ оптимальноњ вартост≥ виконанн€ проекту z *в≥д директивноњ тривалост≥ його виконанн€ Td(6<Td <9), складемо задачу параметричного л≥н≥йного програ≠муванн€, обравши за параметр Td:
«найти t12, t13,t23,T1 “2,“3, що належать област≥ G, визначеноњ умовами:
3 ≤ t12 ≤ 5, 5≤ t13 ≤ 8, 3 ≤ t23 ≤ 4
T1 + t12 ≤ T2, T1 + t13 ≤ T3, T2 + t23 ≤ T3; T1 ≥ 0, T3 ≤ Td
≥ м≥н≥м≥зують функц≥ю ц≥л≥:
z = z12 + z13 + z23,

–озв'€зок задач≥ параметричного програмуванн€ наведено на рис. 10.20. Ѕачимо, зокрема, що коли директивну тривал≥сть прое≠кту обрати такою, що дор≥внюЇ 8 м≥с. (Td = 8), оптимальна вар≠т≥сть виконанн€ проекту дор≥внюватиме 25 тис. грн (z* = 25).

|
–ис. 10.20
ƒос≥ при плануванн≥ проекту враховувалис€ лише витрати, що пов'€зан≥ ≥з скороченн€м терм≥н≥в виконанн€ окремих роб≥т. ƒал≥ опрацюЇмо питанн€ про те, €к додатково врахувати втрати, пов'€зан≥ ≥з затримкою з виконанн€м проекту.
ќтже, нехай Td Ч нормативний терм≥н завершенн€ проекту, s Ч втрати, що пов'€зан≥ ≥з затримкою зак≥нченн€ проекту на одиницю часу понад нормативний терм≥н його виконанн€.
„ас затримки ≥з виконанн€м проекту t обчислюЇтьс€ за фор≠мулою:
t = 
 ,
,
де “n - терм≥н настанн€ к≥нцевоњ n-оњ под≥њ с≥тьового граф≥ка.
“ому додатков≥ витрати через затримку завершенн€ проекту складуть величину st грошових одиниць. ўоб врахувати ц≥ ви≠трати при оптим≥зац≥њ с≥тьового граф≥ка за показником м≥н≥м≥зац≥њ загальноњ вартост≥, до економ≥ко-математичноњ модел≥ (10.12)Ч (10.16) сл≥д ввести так≥ корективи:
1)зам≥нити ц≥льову функц≥ю (10.16) на функц≥ю:
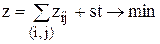
€ка враховуЇ €к витрати, що пов'€зан≥ ≥з виконанн€м проекту (пе≠рший доданок), так ≥ втрати внасл≥док зак≥нченн€ проекту ≥з зап≥≠зненн€м понад нормативний терм≥н Td (другий доданок);
2) обмеженн€ (10.14) (“n  “d) зам≥нити умовами, €к≥ в≥дбива≠ють можлив≥сть зап≥зненн€ ≥з зак≥нченн€м проекту на терм≥н t.
“d) зам≥нити умовами, €к≥ в≥дбива≠ють можлив≥сть зап≥зненн€ ≥з зак≥нченн€м проекту на терм≥н t.
Tn  Td + t, t
Td + t, t  0.
0.
¬ оптимальному план≥ скоригованоњ задач≥ значенн€ t  зм≥нноњ t задовольн€тиме умову:
зм≥нноњ t задовольн€тиме умову:
 =max {0;
=max {0; 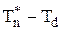 }
}
тобто €вл€тиме собою оптимальний терм≥н можливоњ затримки ≥з завершенн€м проекту понад нормативний терм≥н Td, €кщо це технолог≥чно необх≥дно та економ≥чно виправдано.
|
|
|
10.4 —≥тьове плануванн€ за умов ризику щодо тривалостей операц≥й
” практичному застосуванн≥ с≥тьового плануванн€ виконанн€ проекту часом трапл€ютьс€ ситуац≥њ, коли одна або дек≥лька роб≥т можуть бути не детерм≥нованими. “обто тривал≥сть tij роботи  Ї випадковою величиною з пром≥жку
Ї випадковою величиною з пром≥жку  , €ка маЇ
, €ка маЇ  - розпод≥л з параметрами
- розпод≥л з параметрами 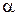 та
та  .
.
‘ункц≥€ щ≥льност≥ ≥мов≥рностей  , розпод≥леноњ на в≥др≥зку aij,bij випадковоњ величини визначаЇтьс€ у вигл€д≥:
, розпод≥леноњ на в≥др≥зку aij,bij випадковоњ величини визначаЇтьс€ у вигл€д≥:
f(t) = B (t Ц aij)a(bij Ц t)y, aij ≤ t ≤ bij,
де ¬, α, γ > 0; ¬ визначаЇтьс€ через параметри розпод≥лу α та γ за формулою:

√раф≥к ц≥Їњ функц≥њ наведено на рис. 10.21
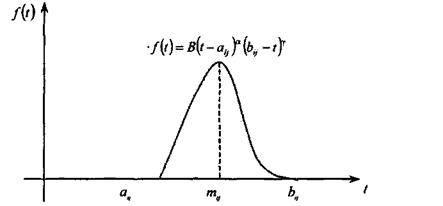
–ис. 10.21
—татистичн≥ характеристики β - розпод≥леноњ випадковоњ ве≠личини обчислюютьс€ за формулами:
- оч≥куване значенн€: 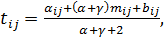
- стандартне в≥дхиленн€: 
де mij Ц модальне (най≥мов≥рн≥ше) значенн€ ц≥Їњ випадковоњ величини.
” метод≥ PERT параметри α ≥ γ приймають значенн€:
α = 2 ±  , γ = 2
, γ = 2 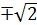 .
.
“аким чином, дл€ знаходженн€ статистичних характеристик випадковоњ величини tij тривалост≥ роботи ≥  j потр≥бно визна≠чити (€к правило, експертним методом) лише три њњ оц≥нки:
j потр≥бно визна≠чити (€к правило, експертним методом) лише три њњ оц≥нки:
Чоптим≥стичну (найменше значенн€) Ч аij,
Чпесим≥стичну (найб≥льше значенн€) Ч bij,
Чмодальну (най≥мов≥рн≥ше значенн€) Ч mij
Ќа основ≥ наведених оц≥нок статистичн≥ характеристики випа≠дковоњ тривалост≥ tij роботи ≥  j обчислюютьс€ за формулами:
j обчислюютьс€ за формулами:
- оч≥куване значенн€:

- стандартне в≥дхиленн€:

якщо тривалост≥ роб≥т не детерм≥нован≥, тривал≥сть “ виконанн€ проекту теж буде не детерм≥нованою, тобто њњ сл≥д розгл€дати €к випадкову величину. —татистичн≥ характеристики ц≥ Ї випадковоњ величини обчислюютьс€ за результатами досл≥дженн€ с≥тьового граф≥ка. якщо у с≥тьовому граф≥ку за тривалост≥ ви конанн€ роб≥т обрати њх оч≥куван≥ значенн€, оч≥кувана тривал≥сть: “ виконанн€ проекту зб≥гатиметьс€ з довжиною в≥дпов≥дною критичного шл€ху.
ƒисперс≥ю  2(т) випадковоњ величини тривалост≥ виконанн€; проекту “ обчислюють у припущенн≥ про статистичну незалежн≥сть випадкових терм≥н≥в виконанн€ окремих роб≥т. ÷€ дисперс≥€ Ї сумою дисперс≥й тривалостей тих роб≥т, €к≥ утворюють критичний шл€х у с≥тьовому граф≥ку з оч≥куваними тривалост€ми виконанн€ роб≥т:
2(т) випадковоњ величини тривалост≥ виконанн€; проекту “ обчислюють у припущенн≥ про статистичну незалежн≥сть випадкових терм≥н≥в виконанн€ окремих роб≥т. ÷€ дисперс≥€ Ї сумою дисперс≥й тривалостей тих роб≥т, €к≥ утворюють критичний шл€х у с≥тьовому граф≥ку з оч≥куваними тривалост€ми виконанн€ роб≥т:

ѕрим≥тка. якщо критичних шл€х≥в дек≥лька, л≥д обрати шл€х ≥з найб≥льшою дисперс≥Їю довжини.
ќск≥льки на тривал≥сть “ виконанн€ проекту впливаЇ велика к≥льк≥сть р≥зних чинник≥в, вводитьс€ припущенн€, що “ Ї норма≠льно розпод≥леною випадковою величиною. ÷е припущенн€ до≠звол€Ї, зокрема, оц≥нювати ≥мов≥рност≥ под≥й завершенн€ проекту до певноњ календарноњ дати або у певний пром≥жок часу. ѕри оц≥≠нюванн≥ под≥бних ≥мов≥рностей корисно пам'€тати про правила с≥гм, €к≥ притаманн≥ нормальному розпод≥лу:
Чправило одн≥Їњ сигми:
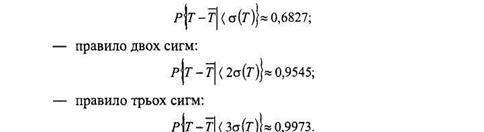
|
ѕриклад 6.6. –озгл€немо проект, €кий складаЇтьс€ з восьми роб≥т. —труктурна схема проекту та оц≥нки тривалостей виконан≠н€ його роб≥т наведено у табл. 10.6.
ѕотр≥бно визначити:
Ч оч≥кувану тривал≥сть виконанн€ проекту;
Ч ≥мов≥рн≥сть под≥њ, що фактична тривал≥сть не перевищуватиме оч≥кувану б≥льше н≥ж на 2 тижн≥.
“абл. 10.6

–озв'€зуванн€. ѕобудуЇмо с≥тьову модель проекту (рис. 10.22) та обчислимо за формулами (10.17), (10.18) статистичн≥ характери≠стики (оч≥куван≥ значенн€ ≥ стандартн≥ в≥дхиленн€) випадко≠вих величин Ч тривалостей виконанн€ кожноњ ≥з роб≥т (див. табл. 10.7).

–ис. 10.22
“абл. 10.7

ѕобудуЇмо с≥тьовий граф≥к проекту, обравши оч≥куванн≥ тривалост≥ виконанн€ роб≥т; обчислимо часов≥ характеристики ус≥х його под≥й (вершин) ≥ позначимо критичний шл€х (рис.10.23).

–ис. 10.23
ритичний шл€х проекту утворюють дуги 1→ 4, 4→ 6 та 6 → 7. “ому оч≥кувана тривал≥сть виконанн€ проекту дор≥внюЇ:
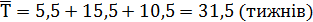
ќбчислимо дисперс≥ю σ2(“) випадковоњ величини “-тривалост≥ виконанн€ проекту:
σ2(“) = 0,832 + 1,832 + 1,832 = 7,4467.
«апитанн€ ≥ завданн€ дл€ самоконтролю
1. Ќазв≥ть основн≥ характеристики задач упор€дкуванн€ та коор≠динац≥њ.
2. —формулюйте задачу календарного плануванн€ та назв≥ть осно≠вн≥ методи њх розв '€зуванн€.
3. Ќазв≥ть сфери застосуванн€ с≥тьових граф≥к≥в.
4. Ќазв≥ть основн≥ елементи с≥тьового граф≥ку та запиш≥ть мето≠дику побудови с≥тьового граф≥ку.
5. ƒайте визначенн€ пон€ть: критичний шл€х, часовий резерв.
6. яка основна ≥де€ методу г≥лок та меж? ¬ чому його особлив≥сть?
7. як виконуЇтьс€ розгалуженн€?
8. як зм≥нюютьс€ значенн€ оц≥нок при розгалуженн≥ множини допустимих розв '€зк≥в на п≥дмножин≥ в метод≥ г≥лок та меж?
|
|
|
9. Ќазв≥ть ознаки одержанн€ замкнутого ≥ оптимального маршру≠т≥в у задач≥ ком≥во€жера.
10. як визначаЇтьс€ критичний шл€х проекту?
11. –озрахуйте часов≥ характеристики роб≥т с≥тьових граф≥к≥в ((≈(≥), L(j), M(i,j), N(i,j) P(i,j)):
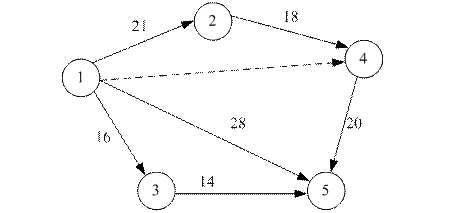
а)

б)
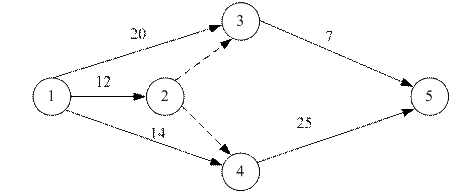
в)

г)






