Силовой расчет механизмов. Определение реакций в кинематических парах.

В задачу силового расчета входит определение всех сил и моментов пар сил, которые приложены к каждому отдельному звену механизма. Эти силы или моменты надо знать, например, для расчета на прочность отдельных звеньев механизма или их частей (деталей).

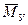Для того чтобы механизм находился в равновесии под воздействием внешних сил, к одному из звеньев его должна быть приложена уравновешивающая сила или уравновешивающая пара сил, характеризуемая ее моментом — уравно­вешивающим моментом. Эту силу или момент 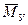обычно считают приложенными к ведущему звену, которое либо получает энергию, потребную для движения меха­низма, извне, как это имеет место у механизмов рабочих машин, либо отдает ее, как это имеет место у механизмов двигателей.

Если при силовом расчете механизма в число известных внешних сил не включена инерционная нагрузка на звенья, то силовой расчет механизма назы­вается статическим. Если же при силовом расчете механизма в число известных внешних сил, приложенных к его звеньям, входит инерционная нагрузка на звенья, то силовой расчет механизма называется кинетостатическим. Для проведения его необходимо знать закон движения ведущего звена, чтобы иметь возможность предварительно определить инерционную нагрузку на звенья.

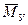Силовой расчет включает: а) определения реакций в кинема­тических парах механизма, б) нахождения уравновешивающих силы или момента . Он производится в следующей последовательности.

1.Определяются все внешние силы, приложенные к звеньям механизма, от действия которых требуется найти реакции в кинематических парах механизма.

2.Определяется точка приложения и направление (линия действия) уравновешивающего усилия или .

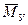3.Проводится силовой расчет каждой группы Ассура в порядке обратном формуле строения механизма.

4. В заключение производится силовой расчет ведущего звена.

Задачи обычно решают графоаналитическим методом, используя уравнения равновесия всей группы или отдельных ее звеньев в форме

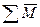, =0.

В число сил и моментов, входящих в эти уравнения, включаются реакции и моменты реакций в кинематических парах группы.

На основании векторных уравнений первого вида строятся многоугольники сил, которые носят название плана сил группы, причем в первую очередь находятся реакции во внеш­них кинематических парах группы, а затем во внутренних парах по условиям равновесия звеньев группы, взятых порознь.

Для реакций, возникающих между элементами кинематических пар, приняты следующие обозначения: реакция со стороны звена k на звено l обозначается R_kl реакция же со стороны звена l на звено k соответственно обозначается R_lk. Оче­видно, что

= – _.

Реакция характеризуется величиной (модулем), направлением и точкой приложения.

Пренебрегая трением в кинематических парах, можно отметить следующее.

Во вращательной паре подлежат определению величина и направление реак­ции, так как ее точка приложения совпадает с осью вращения пары. В поступатель­ной паре подлежат определению величина и точка приложения реакции, так как известно только то, что направление реакции в такой паре всегда перпендикулярно оси ее направ­ляющей.

Пример силового расчета механизма.

Провести силовой расчет заданного положения кривошипно-ползунного механизма компрессора (рис.43, а), если длины звеньев равны 1_АВ = 0,05 м, l_ВС = 0,2 м; положения центров масс звеньев: S₁ =A, l_BS2 = 0,1 м, массы звеньев: т₁ = 0, т₂ = 0,5 кг, т₃ = 0,40 кг; центральный момент инерции шатуна ВС- I_S2 = 0,0018 кгм². Угловая скорость кривошипа АВ постоянна и равна ω₁ = 80 сек^-1. Сила полезного сопротивления равна Р_С =250 Н, она противоположна (см. рис. 42 а,б) и проходит через точку С; сила тяжести шатуна - G₂ = m₂g = 0,5*10 = 5 н, сила тяжести ползуна - G₃ = m₃g = 0,4*10 = 4 н. Уравновешивающая сила приложена перпендикулярно звену 1 в точке А.

Подлежит определению: реакция в поступательной кинематической паре С, которая направлена перпендикулярно линии хода ползуна;реакция во вращательной паре С; реакция во вращательной паре В; реакция во вращательной паре А и уравновешивающая сила , приложенная к звену 1.

Решение. 1. Все внешние силы, действующие на звенья механизма, заданы, поэтому этот этап расчета выполнен.

2.Уравновешивающая сила Р_У приложена перпендикулярно звену 1 в его точке В.

3. Механизм содержит только одну группу Ассура Л.В., состоящую
из звеньев 2 и 3. Эта группа относится ко второму классу второго вида,

Составляем уравнения равновесия группы. Разложим реакцию на две составля­ющих: , направленную перпендикулярно линии ВС, и , направленную по линии ВС. Тогда геометрическая сумма сил, приложенных к группе (рис.43, б), равна

+ + + + + + + = 0

В качестве второго уравнения взято уравнение =0, которое, будучи развернутым, примет вид

l_ВС + G₂ h_G2 –P_И2h_РИ2 – М_И2 =0,

откуда

= = 54 Н,

где h_G2 = 0,09 м - плечо силы G₂ относительно точки С (найдено по чертежу).

h_РИ2 = 0,07 м - плечо силы P_И2 относительно точки С (найдено по чертежу).

Строим план сил группы (рис. 43, в) в масштабе μ_Р = 2 н/мм.

Порядок построения векторной суммы, вообще говоря, безразличен, но при­менительно к данной группе Ассура можно рекомендовать следующий: проводим прямую, параллельную ВС. Это будет линия действия силы .Отложим от произвольной точки а, лежащей на этой прямой(рис. 43, в),силу в виде

отрезка (аb)= = = 27 мм, перпендикулярно прямой.От точки b откладываем силу в виде отрезка (bс) = = = 2,5 мм, далее от точки с откладываем силу в виде отрезка (cd) = = = 60 мм. Из точки d откладываем силу в виде отрезка (de) = = =44 мм., далее от точки e откладываем силу в виде отрезка (ef) = = =2 мм. Силу откладываем в виде отрезка (fg)= = = 125 мм. Силы откладываем в соответствии с их направлениями на чертеже группы. 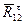И, наконец, из точки g восстанавливаем перпендикуляр (линия действия силы ) до пересечения с линией действия силы Полученная точка k– начало вектора . Отрезок (kа) в масштабе μ_Р дает искомую реакцию , а отрезок (gk) в том же масштабе — реакцию , а отрезок (kb) дает искомую реакцию .

Для нахождения реакции напишем условие равновесия звена 2:

+ + + = 0

Из плана сил (рис. 43, в) видно, что отрезок (dk) в масштабе μ_Р соответствует иско­мой реакции . Реакция должна проходить через точку С.

5) Силовой расчет ведущего звена 1 (рис.43, г). К звену 1 приложены: сила =- (ее величина определяется из плана сил (рис. 7, в) отрезком (kb), сила = (kb) μ_Р = 65*2 = 130 Н, сила (реакция) , приложенная в точке А и уравновешивающая сила Р_У, приложенная перпендикулярно звену 1 в точке В. Из равенства нулю суммы моментов относительно точки А сил, приложенных к звену 1, находим величину уравновешивающей силы Р_У

- Р_У l_AB + R₂₁ h₂₁ = 0,

где h₂₁ (плечо cилы ) находится по чертежу (рис. 43, г).

Р_У = = =125Н

Условием равенства нулю векторной суммы сил, приложенных к звену 1, будет

+ + = 0.

Отсюда находим модуль реакции путем построения векторного треугольника сил (рис. 43, д): R₀₁ = (bc) μ_Р (Н).

 

Рис.43. Силовой расчет кривошипно-ползунного механизма компрессора. а) положение механизма; б) структурная группа с приложенными силами; в) план сил.

 

Определив величину (М_у) момента уравновешивающей пары сил, можно найти мощность двигателя, необходимую для привода машины. Для этого нужно знать (ω₁) угловую скорость кривошипа 1.