Контур с током в магнитном поле

МОЩНОСТЬ ПОСТОЯННОГО ТОКА

- отношение работы тока за время t к этому интервалу времени.

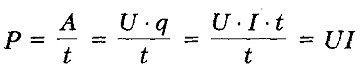
В системе СИ:

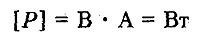
20) Итак, по двум длинным прямым параллельным проводникам (рис. 440), находящимся на расстоянии R друг от друга (которое во много, раз в 15 меньше длин проводников), протекают постоянные токи I₁, I₂.

 

рис. 440

 В соответствии с полевой теорией взаимодействие проводников объясняется следующим образом: электрический ток в первом проводнике создает магнитное поле, которое взаимодействует с электрическим током во втором проводнике. Чтобы объяснить возникновение силы, действующей на первый проводник, необходимо проводники «поменять ролями»: второй создает поле, которое действует на первый. Повращайте мысленно правый винт, покрутите левой рукой (или воспользуйтесь векторным произведением) и убедитесь, что при токах текущих в одном направлении, проводники притягиваются, а при токах, текущих в противоположных направлениях, проводники отталкиваются¹.
 Таким образом, сила, действующая на участок длиной Δl второго проводника, есть сила Ампера, она равна

 

где B₁ − индукции магнитного поля, создаваемого первым проводником. При записи этой формулы учтено, что вектор индукции B₁ перпендикулярен второму проводнику. Индукция поля, создаваемого прямым током в первом проводнике, в месте расположения второго, равна

 

 Из формул (1), (2) следует, что сила, действующая на выделенный участок второго проводника, равна

 

 Легко убедится, что такая же по модулю сила действует на участок такой же длины первого проводника. В этом можно убедиться, просто взглянув внимательно на полученный результат (3) − силы токов входят в эту формулу симметрично. Таким образом, силы взаимодействия между проводниками удовлетворяют третьему закону Ньютона.
 Можно наглядно проиллюстрировать взаимодействие проводников, построив картины силовых линий магнитных полей, создаваемых двумя параллельными проводниками. Если мы умеем рассчитывать поля, то по известному алгоритму можно построить эти силовые линии, затратив немного усилий. Вспомним также, что основоположник теории электромагнитного поля Майкл Фарадей воспринимал силовые линии (магнитного и электрического полей) как упругие трубки, благодаря натяжению которых и возникают силы взаимодействия. Ниже представлены точно рассчитанные картины силовых линий магнитных полей в плоскости перпендикулярной двум длинным проводникам, по которым протекают постоянные электрические токи.
Так на рис. 441 показаны силовые линии, для токов текущем в одном направлении, на рис. 441 а силы токов равны, а на рис. 441 б различны. Не правда ли − эти «упругие трубки» стягивают проводники?

 

 

рис. 441

 На рис. 442 токи текут в противоположных направлениях, в обоих случаях силы токов различны. Здесь проводникам явно не нравится находиться рядом − они стремятся разойтись.

 

21) Магни́тная инду́кция {\displaystyle {\vec {B}}} — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой {\displaystyle {\vec {F}}} магнитное поле действует на заряд {\displaystyle q}, движущийся со скоростью {\displaystyle {\vec {v}}}.

Более конкретно, {\displaystyle {\vec {B}}} — это такой вектор, что сила Лоренца {\displaystyle {\vec {F}}}, действующая со стороны магнитного поля^[1] на заряд {\displaystyle q}, движущийся со скоростью {\displaystyle {\vec {v}}}, равна

{\displaystyle {\vec {F}}=q[{\vec {v}}\times {\vec {B}}]}

{\displaystyle F=qvB\sin \alpha }

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора {\displaystyle {\vec {F}}} перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 10⁴ Гс

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния ихдвижения^[1]; магнитная составляющая электромагнитного поля^[2].

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты).

22) Сила Лоренца Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды. Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца.

· 23) Сила Ампера — это сила, с которой магнитное поле действует на помещенный в него проводник с током.

Согласно экспериментальным данным модуль силы F:

пропорционален длине проводника l, находящегося в магнитном поле;

пропорционален модулю индукции магнитного поля B;

пропорционален силу тока в проводнике I;

зависит от ориентации проводника в магнитном поле, т.е. от угла α между направлением тока и вектора индукции магнитного поля B⃗ B→.

Тогда:

модуль силы Ампера равен произведению модуля индукции магнитного поля B, в котором находится проводник с током, длины этого проводника l, силы тока I в нем и синуса угла между направлениями тока и вектора индукции магнитного поля

FA=I⋅B⋅l⋅sinα FA=I⋅B⋅l⋅sin⁡α,

 

 

24) Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества (источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки; элементарным источником магнетизма считают замкнутый ток). Магнитным моментом обладаютэлементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина.

Магнитный момент измеряется в А⋅м² или Дж/Тл (СИ), либо эрг/Гс (СГС), 1 эрг/Гс = 10⁻³ Дж/Тл. Специфической единицей элементарного магнитного момента является магнетон Бора.

Контур с током в магнитном поле

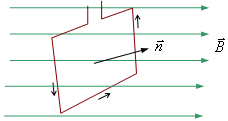Рис. 4.13

Пусть в однородное магнитное поле помещена рамка с током (рис. 4.13). Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором и нормалью к площади :

.

Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке.

Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:

.

Это выражение также можно использовать для определения индукции магнитного поля:

.

Величину, равную произведению , называют магнитным моментом контура Р_т. Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать

.

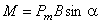При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.

 

25) Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока на изменение магнитного потока: , где 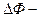изменение магнитного потока, сцепленного с контуром или магнитный поток через поверхность, прочерченную контуром. Формула справедлива для контура любой формы в произвольном магнитном поле.

 

Магнитное поле соленоида

Соленоидом называют катушку цилиндрической формы из проволоки, витки которой намотаны вплотную в одном направлении, а длина катушки значительно больше радиуса витка.

Магнитное поле соленоида можно представить как результат сложения полей, создаваемых несколькими круговыми токами, имеющими общую ось. На рисунке 3 видно, что внутри соленоида линии магнитной индукции каждого отдельного витка имеют одинаковое направление, тогда как между соседними витками они имеют противоположное направление.

Рис. 3

Поэтому при достаточно плотной намотке соленоида противоположно направленные участки линий магнитной индукции соседних витков взаимно уничтожаются, а одинаково направленные участки сольются в общую линию магнитной индукции, проходящую внутри соленоида и охватывающую его снаружи.Изучение этого поля с помощью опилок показало, что внутри соленоида поле является однородным, магнитные линии представляют собой прямые линии, параллельные оси соленоида, которые расходятся на его концах и замыкаются вне соленоида (рис. 4).

Рис. 4

Нетрудно заметить сходство между магнитным полем соленоида (вне его) и магнитным полем постоянного стержневого магнита (рис. 5). Конец соленоида, из которого магнитные линии выходят, аналогичен северному полюсу магнита N, другой же конец соленоида, в который магнитные линии входят, аналогичен южному полюсу магнита S.

Рис. 5

Полюсы соленоида с током на опыте легко определить с помощью магнитной стрелки. Зная же направление тока в витке, эти полюсы можно определить с помощью правила правого винта: вращаем головку правого винта по току в витке, тогда поступательное движение острия винта укажет направление магнитного поля соленоида, а следовательно, и его северного полюса. Модуль магнитной индукции внутри однослойного соленоида вычисляется по формуле

B=μμ0NIl=μμ0nl, B=μμ0NIl=μμ0nl,

где Ν — число витков в соленоиде, I — длина соленоида, n — число витков, приходящееся на единицу длины соленоида.

 

27) Магне́тик, термин, применяемый ко всем веществам при рассмотрении их магнитных свойств. Из-за различий магнитных свойств микрочастиц, образующих вещество, а также характера взаимодействия между ними, выделяют несколько типов магнетиков, которые классифицируют по величине и знаку магнитной восприимчивости; различают ферромагнетики, ферримагнетики, антиферромагнетики,парамагнетики, диамагнетики. Физическая классификация магнетиков основана на рассмотрении природы микрочастиц, обладающих магнитными моментами, их взаимодействия в веществе, а также влияния на магнетики внешних факторов.

28) Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе^[1].

Магнитная восприимчивость определяется отношением намагниченности единицы объёма вещества к напряжённости намагничивающего магнитного поля. По своему смыслу восприимчивость являетсявеличиной безразмерной.

{\displaystyle \chi ={\frac {J}{H}}}, где {\displaystyle J} — намагниченность вещества под действием магнитного поля, {\displaystyle H} — напряженность магнитного поля.

Иногда бывает полезно также ввести понятие удельной магнитной восприимчивости, равной восприимчивости единицы массы вещества. В СИ удельная восприимчивость измеряется в обратныхкилограммах (кг⁻¹). Аналогично, молярная магнитная восприимчивость определяется как восприимчивость одного моля вещества и измеряется в обратных молях (моль⁻¹).

Магнитная проницаемость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией {\displaystyle {B}} и напряжённостью магнитного поля {\displaystyle {H}} в веществе. Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая её состав, состояние, температуру и т. д.).

Впервые встречается в работе Вернера Сименса «Beiträge zur Theorie des Elektromagnetismus» («Вклад в теорию электромагнетизма») в 1881 году^[1].

Обычно обозначается греческой буквой {\displaystyle \mu }. Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных).

29) Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.

Магнитным потоком Φ через площадь S контура называют величину

Φ = B · S · cos α,

где B – модуль вектора магнитной индукции, α – угол между вектором и нормалью к плоскости контура (рис. 1.20.1).

Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.

30) Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года.

31) токами Фуко называется Индукционный ток, который имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток

Индукционный ток — электрический ток, возникающий в замкнутом проводящем контуре при изменении потока магнитной индукции, пронизывающего этот контур. Величина и направление индукционного тока определяются законом электромагнитной индукции и правилом Ленца.

32) САМОИНДУКЦИЯ

Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.

При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.

Это явление называется самоиндукцией.
Самоиндукция - явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.
Возникающая при этом ЭДС называется ЭДС самоиндукции

ИНДУКТИВНОСТЬ

От чего зависит ЭДС самоиндукции?

Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике
(B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I).
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника
(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.

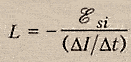
Индуктивность - физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:

где Ф - магнитный поток через контур, I - сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от:
числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды
(возможен сердечник).

33)