Динамические характеристики Земли

Динамические параметры Земли – важнейшие её характеристики – определяются тензором инерции Земли, определённым на эпоху установления системы координат и закона распределения масс в теле Земли.

Матрица вторых моментов инерции

(1.1)

называется тензором инерции второго ранга.

Моментом инерции тела относительно оси называется величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси, равная сумме произведений масс всех частей тела на квадраты их расстояний от той же оси. Моменты инерции твёрдого тела относительно некоторой оси зависят только от формы тела и от распределения масс относительно этой оси.

В системе координат, ось w которой совмещена с мгновенной осью вращения тела, ось u направлена в точку пересечения плоскостей экватора и меридиана с долготой λ ₀, ось v дополняет правую систему координат (рис.1.29), моменты инерции второго порядка относительно этих осей вычисляются по формулам:

(1.2)

где u, v, w – координаты элементарной частицы тела dm.

Центробежные моменты инерции тела по отношению к осям O u, O v, O w определяются по формулам:

(1.3)

Момент инерции для тела конечной массы имеет величину конечную и отличную от нуля.

Уравнение

(1.4)

есть уравнение эллипсоида конечных размеров в точке О. Следовательно, тензор инерции второго ранга (1.1) однозначно определяет трёхосный эллипсоид. Геометрический образ тензора инерции второго ранга называется эллипсоидом инерции твёрдого тела.

В частном случае тензор инерции второго ранга, составляющими которого являются вторые моменты инерции Земли в геоцентрической системе отсчёта, есть тензор инерции Земли, и он же определяет эллипсоид инерции Земли.

Центральным эллипсоидом инерции твёрдого тела называется эллипсоид инерции, соответствующий центру инерции этого тела.

Любой эллипсоид имеет главные оси. Главные оси центрального эллипсоида инерции тела называются главными центральными осями инерции, а моменты инерции тела относительно этих осей – главными центральными моментами инерции.

Если квадраты полуосей эллипсоида , то его уравнение в главных осях будет

. (1.5)

Сравнивая его с уравнением (1.4), замечаем, что центробежные моменты относительно главных осей равны нулю.

В геодезических задачах главные оси проходят через центр инерции Земли и называются главными центральными осями инерции Земли. Моменты инерции относительно этих осей называются главными центральными моментами инерции и обозначаются .

Тензор инерции в главных осях есть диагональная матрица, составленная из главных моментов инерции

. (1.6)

Главный тензор инерции (1.6) не зависит от принятой системы координат и является фундаментальным параметром планетарного тела. Он зависит только от распределения масс внутри тела. Определение фундаментальных параметров планетарного тела является особой задачей геодезии.

За динамическую фигуру Земли принимают центральный эллипсоид инерции Земли, оси которого совмещены с главными центральными осями, а его центр совпадает с центром инерции. Поиск главных центральных моментов инерции сводится к решению векового уравнения

(1.7)

корнями которого и являются главные центральные моменты инерции . Полуоси трёхосного эллипсоида инерции равны

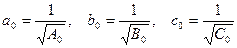. (1.8)

Полярное и экваториальное сжатие динамической фигуры определяется соответственно

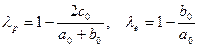. (1.9)

Динамическое сжатие

. (1.10)

Большая полуось динамической фигуры совпадает с осью, относительно которой главный момент инерции 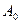минимален, малая ось совпадает с полярной осью, относительно которой главный момент инерции максимален.

Для Земли

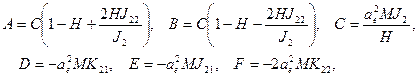(1.11)

где - экваториальный радиус и масса Земли, - гравитационные постоянные Земли.

Углы Эйлера ψ – угол прецессии, φ – угол чистого вращения, θ – угол нутации (рис.1.29), ориентирующие главные оси u, v, w динамической фигуры относительно геоцентрической системы Oxyz, вычисляются по формулам:

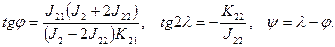(1.12)

Следовательно, если известны моменты инерции планетарного тела относительно принятой системы координат, то можно определить его динамическую фигуру в образе трёхосного эллипсоида инерции и ориентацию её главных осей. По вариациям главных моментов инерции и изменению ориентировки осей эллипсоида инерции во времени можно судить о планетарных изменениях фигуры и перемещениях масс внутри планетарного тела.

Рис.1.29. Ориентирование систем координат углами Эйлера

 

Периодические планетарные изменения динамической фигуры Земли обусловлены деформациями от сил притяжения в системе Солнце-Земля-Луна. Эти изменения с необходимой точностью могут быть предвычислены и учтены в геодезических и астрономических расчётах.

Реальная Земля не является абсолютно твёрдым телом. Центр её масс не занимает постоянного положения из-за перемещения масс в теле и на поверхности Земли. Перемещение масс в теле Земли должно приводить к изменению тензора инерции и, следовательно, к изменению значений главных центральных моментов инерции Земли (табл.2) и ориентации её главных центральных осей инерции в теле Земли.

Для планетарной геодезии важна оценка взаимного положения инерциальных, средних и мгновенных полюсов Земли. Инерциальный полюс – это точка пересечения главной центральной оси инерции, относительно которой Земля обладает максимальным главным центральным моментом инерции, с телом Земли. В теории фигуры Земли, а также при установлении параметров уровенного эллипсоида, наилучшим образом аппроксимирующего планетарный геоид, необходимо ось вращения уровенного эллипсоида совмещать с главной центральной осью инерции Земли, а его центр – с центром инерции Земли.

Динамическая и гравитационная модели Земли отличаются друг от друга. Динамическое сжатие Н не равно гравитационному сжатию a. Эти различия в полном спектре необходимо учитывать при изучении вращения Земли вокруг своей мгновенной оси. Близость инерциальных и средних полюсов облегчает изучение движения полюсов Земли. В этом случае это движение будет отождествлено с движением мгновенного полюса относительно полюса инерции Земли.

Если оси земной системы координат совпадают с главными центральными осями инерции Земли, то должно соблюдаться условие Во всех моделях Земли эти коэффициенты незональных гармоник первого и второго порядков отличаются от нуля. Следовательно, оси земной системы координат не совпадают с главными центральными осями инерции, а средний полюс не совпадает с полюсом инерции.

Однако коэффициенты настолько малы, что центробежные моменты и каждый по модулю в 10⁸ раз меньше, чем главные моменты. Это признак близости среднего и инерциального полюсов и малости угла . Из-за малости этого угла долготу главной центральной оси инерции, относительно которой Земля обладает наименьшим главным моментом инерции, можно вычислять как сумму двух эйлеровых углов по формуле (1.12).

В 1928г. английский астроном и геофизик Джеффрис впервые указал на возможное влияние земных приливов на изменение скорости вращения Земли. Приливы приводят к возникновению трения и уменьшению со временем угловой скорости вращения Земли. Вариации скорости происходят почти исключительно из-за изменений наибольшего момента инерции Земли.

Основные параметры динамической фигуры Земли достаточно надёжно определяются по моделям её внешнего гравитационного поля. Определение фундаментальных параметров Земли – главного тензора инерции (1.6) и эйлеровых углов главных осей динамической фигуры Земли (1.12) – необходимо на эпоху, на которую определены вторые гармонические коэффициенты геогравитационного потенциала. При этом они должны быть согласованы с масштабом, в смысле , принятым в смежных науках о Земле и космическом пространстве. Только в этом случае эти параметры можно использовать в общем комплексе с другими постоянными Земли, других планет и тел космического пространства и изучать их изменения во времени.