Лекция 7.
Рассматривая задачу о частице в потенциальной яме, мы считали, что на границах ямы волновая функция становится равной нулю и вероятность обнаружить частицу за пределами ямы также равна нулю. В действительности дело обстоит значительно сложнее и имеется определенная вероятность обнаружить электрон за пределами потенциальной ямы. Этот результат существенно отличается от выводов классической физики. Частица, подчиняющаяся законам классической физики, может выйти из потенциальной ямы только при условии, что ее полная энергия превышает «глубину» потенциальной ямы. Стенки потенциальной ямы представляют для частицы потенциальный барьер, который она не может преодолеть. Для того чтобы частица могла выйти из потенциальной ямы или проникнуть в нее, согласно классической физике, ей нужно сообщить энергию, большую высоты потенциального барьера.
Квантовая механика приводит к принципиально новому выводу о возможности прохождения частиц сквозь потенциальные барьеры. Это явление называется туннельным эффектом.
Пусть частица, движущаяся по оси x, встречает на своем пути простейший потенциальный барьер прямоугольной формы высотой U0 и шириной l.
По классическим законам, если кинетическая энергия частицы больше высоты барьера E > U0, т. е. потенциальной энергии в области II, то частица беспрепятственно проходит эту область. При этом ее кинетическая энергия и скорость уменьшаются над барьером, а затем при x > l снова принимают свое значение. Если E < U0, то частица отражается от барьера и летит в обратную сторону.
Поведение микрочастицы можно определить, решая уравнение Шредингера. Физический интерес представляет случай, когда полная энергия частицы меньше высоты потенциального барьера E < U0, поскольку в этом случае классическая физика не разрешает проникнуть частице сквозь барьер.
Для областей I и III
,
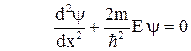для области II
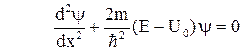
Решение уравнения Шредингера в области I имеет вид
,
в области III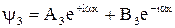 
, где 
.
В области II 
, где 
Решение вида 
соответствует волне, распространяющейся в положительном направлении оси x, а решение вида 
- волне, распространяющейся в противоположном направлении. Решение вида 
соответствует возрастающей экспоненте,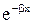 
- убывающей. Характер поведения функций проиллюстрируем рисунком. Видно, волновая функция не равна нулю и внутри барьера, а в области III, если барьер не слишком широк, будет опять иметь вид волн де Бройля с той же длиной волны, но с меньшей амплитудой.
Для нахождения коэффициентов А и В воспользуемся граничными условиями, которым должна удовлетворять ψ- функция. Для того, чтобы пси-функция была непрерывна во всей рассматриваемой области по x, т.е. от - ∞ до + ∞, должны выполняться условия
и 
.
Для того, чтобы функция была гладкой
.
Отношение квадратов модулей амплитуд отраженной и падающей волны
определяет вероятность отражения частицы от потенциального барьера и носит название коэффициента отражения.
Отношение квадратов модулей амплитуд прошедшей и падающей волны
определяет вероятность прохождения частицы через потенциальный барьер и может быть названо коэффициентом прохождения или коэффициентом прозрачности. Он определяет отношение плотности потока прошедших частиц к плотности потока частиц падающих.
Коэффициенты связаны между собой соотношением R + D = 1.
Дальнейшие расчеты приведут нас к следующему выражению для коэффициента прозрачности
.
Из полученного выражения следует, что вероятность прохождения частицы через потенциальный барьер зависит от ширины барьера и массы частицы. С увеличением массы частицы вероятность прохождения уменьшается. На вероятность прохождения также влияет превышение потенциального барьера над энергией частицы, т.е. U0 – E.
В случае потенциального барьера произвольной формы
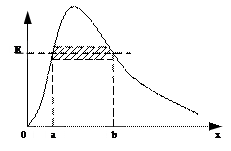При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере, в связи с чем это явление и получило название туннельного эффекта.
С классической точки зрения частица, «находящаяся в туннеле», должна обладать отрицательной кинетической энергией (E < U). Однако туннельный эффект явление специфически квантовое, не имеющее аналога в классической физике. В квантовой механике деление энергии на кинетическую и потенциальную не имеет смысла, так как противоречит соотношению неопределенности.
Прохождение частиц сквозь потенциальный барьер нашло экспериментальное подтверждение в явлении автоэлектронной эмиссии электронов из металла. Вырывание электронов происходит при напряженностях электрического поля, в сотни раз меньших, чем те которые необходимы для того, чтобы электрон преодолел поверхностную разность потенциалов на границе металл-вакуум и покинул металл. Туннельный эффект играет основную роль в явлениях радиоактивного альфа-распада.
Туннельный эффект уже давно весьма эффективно используется в науке и технике. На нем основан принцип действия многих полупроводниковых приборов (туннельные диоды). Он используется в сверхчувствительных записывающих головках магнитных дисков, сканирующих туннельных микроскопах (1981). В настоящее время пространственная разрешающая способность таких микроскопов ~ 20 нм. Для сравнения, современный оптический микроскоп, конструкция которого была изобретена в 1873 г., имеет разрешающую способность ~ 200 нм.
