¬ исходную систему неравенств, представл€ющих собой ограничени€ на все три вида сырь€

 (11.1)
(11.1)
 (11.2)
(11.2)
 (11.3)
(11.3)
 введем дополнительные переменные с коэффициентами = 1 и с нулевым коэффициентом в целевую функцию. ƒополнительные переменные рассматриваютс€ как показатели недоиспользовани€ имеющегос€ сырь€ (ресурсов). “огда неравенства (11) можно записать как систему равенств
введем дополнительные переменные с коэффициентами = 1 и с нулевым коэффициентом в целевую функцию. ƒополнительные переменные рассматриваютс€ как показатели недоиспользовани€ имеющегос€ сырь€ (ресурсов). “огда неравенства (11) можно записать как систему равенств
 (12.1)
(12.1)
 (12.2)
(12.2)
 (12.3)
(12.3)
÷елева€ функци€ при этом примет вид
 (13)
(13)
где  ,
,  ,
,  - количество недоиспользованного ресурса 1-го, 2-го и 3-го видов сырь€.
- количество недоиспользованного ресурса 1-го, 2-го и 3-го видов сырь€.
ѕримем  ,
,  ,
,  как базисные переменные, а ’1 и ’2 Ц как небазисные переменные. Ёто св€зано с тем, что в допустимом множестве, представл€ющем собой многоугольник ќј¬—D (см. рис. 1), в самом начале решени€ все известно лишь в начале осей координат, где ’1=0; ’2 =0. ѕоскольку сырье еще не запущено в производство и ресурсы оказались не тронутыми, то можно записать:
как базисные переменные, а ’1 и ’2 Ц как небазисные переменные. Ёто св€зано с тем, что в допустимом множестве, представл€ющем собой многоугольник ќј¬—D (см. рис. 1), в самом начале решени€ все известно лишь в начале осей координат, где ’1=0; ’2 =0. ѕоскольку сырье еще не запущено в производство и ресурсы оказались не тронутыми, то можно записать:  =7200,
=7200,  =9900,
=9900,  =12600. »менно с этой точки и начинаетс€ процедура решени€, а первый допустимый план принимает вид: ’1=0; ’2 =0;
=12600. »менно с этой точки и начинаетс€ процедура решени€, а первый допустимый план принимает вид: ’1=0; ’2 =0;  =7200,
=7200,  =9900,
=9900,  =12600.
=12600.
ѕосле получени€ первого базисного решени€ ввод€тс€ одна за другой переменные, которые увеличивают значение целевой функции до тех пор, пока не будет получено оптимальное решение. ѕереход от первого базисного плана к последующим осуществл€етс€ путем составлени€ симплексных таблиц.
ѕерва€ таблица (таблица 1) рассматриваетс€ как запись условий задачи и первого варианта решени€.
“аблица 1. ѕервый план решени€ задачи
| Cj | Ѕазис. перем. | ѕлан | |||||
| ’1 | ’2 | ’3 | ’4 | ’5 | |||
| ’3 | |||||||
| ’4 | |||||||
| ’5 | 4,80 | ||||||
| Zj - Cj | -45 | -27 |
¬ первом столбце таблицы записываютс€ стоимости —j целевой функции. ¬о втором Ц базисные переменные  ,
,  ,
,  . »х стоимости —j как вида продукта - нулевые. Ќачина€ с третьего столбца, перва€ строка делитс€ пополам. ¬ нижней части этой строки последовательно записываютс€ все переменные ’i, а в верхней - все коэффициенты целевой функции (13) при этих переменных. «атем в следующих нижних трех строках под этими переменными записываетс€ матрица коэффициентов левой части системы уравнений (12). Ќижн€€ строка называетс€ индексной. аждый ее элемент
. »х стоимости —j как вида продукта - нулевые. Ќачина€ с третьего столбца, перва€ строка делитс€ пополам. ¬ нижней части этой строки последовательно записываютс€ все переменные ’i, а в верхней - все коэффициенты целевой функции (13) при этих переменных. «атем в следующих нижних трех строках под этими переменными записываетс€ матрица коэффициентов левой части системы уравнений (12). Ќижн€€ строка называетс€ индексной. аждый ее элемент  находитс€ по формуле:
находитс€ по формуле:
 (14)
(14)
где  (15)
(15)
 - коэффициенты таблицы i -той строки и j -того столбца.
- коэффициенты таблицы i -той строки и j -того столбца.
ѕоскольку в первой таблице ’1=0; ’2 =0, то zj =0 и, следовательно, коэффициенты:  поэтому в нижней строке все коэффициенты целевой функции (13), ранее записанные в верхней строке, оказываютс€ со знаком минус.
поэтому в нижней строке все коэффициенты целевой функции (13), ранее записанные в верхней строке, оказываютс€ со знаком минус.
¬ектор Ц столбец описывает выпуск соответствующего вида продукта (соответствующий технологический способ). Ёлементы индексной строки характеризуют эффективность технологического способа по отношению к сложившейс€ структуре производства. ≈сли задача решаетс€ на max, то оценка (+) в индексной строке показывает, на сколько уменьшаетс€ прибыль при включении в план соответствующего технологического способа. ѕри (-) оценке наблюдаетс€ увеличение прибыли при включении в план этого способа. ≈сли же задача решаетс€ на min, то результаты оказываютс€ обратными.
|
|
|
“аким образом, при решении задач на max отсутствие в индексной строке (-) оценки свидетельствует о том, что получено оптимальное решение. ¬ противном случае возможно улучшение плана. “огда выбирают наибольшую по абсолютной величине (-) оценку и в новый план ввод€т технологический способ, соответствующий этой оценке. —толбец с наибольшей по абсолютной величине (-) оценкой называетс€ ключевым. ¬ первом плане решени€ задачи (таблица 1) ключевым €вл€етс€ столбец ’1.
ƒл€ удобства воспри€ти€ процедуры обработки симплекс-таблиц выделим вариативную часть таблицы 1 и продемонстрируем этап обработки данных на примере (см. табл. 1.1) упрощенного аналога первой таблицы. ¬ этой таблице выделим жирным шрифтом ключевой столбец h, который соответствует столбцу продукта ’1 с индексом j = 2. ƒалее построчно разделим элементы столбца j = 1 свободных членов (столбец план в табл. 1) на построчно соответствующие элементы ключевого столбца. —трока r (табл.1.2) с наименьшим частным выдел€етс€ жирным шрифтом и называетс€ ключевой. Ёта строка (i = 1) указывает на то, кака€ из переменных должна быть выведена из последующего плана (в данном случае переменна€ ’3), а вместо нее в новый план должна быть введена переменна€ ключевого столбца (переменна€ ’1).
Ёлемент, лежащий на пересечении ключевых столбца и строки, называетс€ главным ключевым элементом (√ Ё).
—одержимое каждой клетки вариативной части матрицы (табл.1.1) обозначим как ij. “огда содержимое √ Ё дл€ первой таблицы 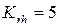 . ѕредставление информации в форме таблицы 1.1 дает возможность подготовить рекуррентные формулы дл€ расчета ij дл€ последующих таблиц.
. ѕредставление информации в форме таблицы 1.1 дает возможность подготовить рекуррентные формулы дл€ расчета ij дл€ последующих таблиц.
“аблица 1.1. ”прощенный аналог таблицы 1
| —толбцы j | |||||||
| 2 = h | |||||||
| —троки i | 1 = r | ||||||
| 9900 | 4 | 0 | 1 | 0 | |||
| 12600 | 4,80 | 6 | 0 | 0 | 1 | ||
| 0 | -45 | -27 | 0 | 0 | 0 |
«аполнение второй симплекс-таблицы (табл. 2) начинаетс€ с ключевой строки по рекуррентной формуле:
 . (16)
. (16)
Ќапример, в табл. 1.1 r Ц ключева€ строка (i=1=r); h Ц ключевой столбец (j=2=h). “огда 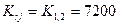 - старое содержимое клетки;
- старое содержимое клетки;  - (√ Ё);
- (√ Ё);  - новое значение содержимого клетки, которое в табл. 2 записываетс€ вместо 7200. ƒл€ клетки √ Ё формула (16) примет вид:
- новое значение содержимого клетки, которое в табл. 2 записываетс€ вместо 7200. ƒл€ клетки √ Ё формула (16) примет вид:
 .
.
“аким образом, в клетках √ Ё результат всегда будет равен 1.
—одержимое остальных клеток вариативной части таблицы заполн€ютс€ по формуле:
 (17)
(17)
Ќапример, в табл. 1 содержимое клетки Ki,j = K4,3 = - 27. ƒл€ расчета нового содержимого этой клетки потребуютс€ следующие данные из табл. 1:
r,j=K1,3=2; Ki,h=K4,2=-45;  ; Ki,j = K4,3 = - 27. (18)
; Ki,j = K4,3 = - 27. (18)
ѕодставив исходные данные (18) в формулу (17), получим число:
 (19)
(19)
которое запишетс€ во вторую симплекс-таблицу 2. “аким же образом заполн€ютс€ остальные клетки второй симплекс-таблицы.
“аблица 2. ¬торой план решени€ задачи (втора€ симплекс-таблица)
| Cj | Ѕазис. перем. | ѕлан | ’1 | ’2 | ’3 | ’4 | ’5 |
| ’1 | 0,4 | 0,2 | |||||
| ’4 | 1,6 | -1,2 | |||||
| ’5 | 4,08 | -0,96 | |||||
| Zj - Cj | -9 |
|
|
|
¬ результате решени€ второго плана получено значение целевой функции F(X) = 64800, располагаемое в индексной строке столбца Ђѕланї и определ€емое как
 . (20)
. (20)
¬ таблице 2 в индексной строке столбца ’2 оказалось отрицательное число (-9), что свидетельствует о возможности улучшени€ плана за счет введени€ в новый план переменной ’2. Ётот столбец выдел€етс€ как ключевой h.
ѕострочно разделим элементы столбца свободных членов, образующих Ђѕланї в табл. 2, на соответствующие элементы ключевого столбца. лючевой строкой r (табл. 2) с наименьшим частным оказалась строка переменной ’4, что означает необходимость вывода из последующего плана этой переменной. ¬место нее в новый план должна быть введена переменна€ ’2.
ƒалее, как и в предыдущем случае, заполн€етс€ таблица 3.
“еперь в индексной строке последней таблицы 3 нет отрицательных чисел, что свидетельствует о том, что экстремум (в данном случае max) целевой функции достигнут.
¬се результаты расчетов наход€тс€ в столбце Ђѕланї и в индексной строке таблицы 3. ¬ соответствии с этими результатами оптимальный план по выпуску продуктов должен составл€ть: 
 = 1125 единиц продукта 1-го вида и
= 1125 единиц продукта 1-го вида и  = 787 Ц целых единиц продукта 2-го вида. ѕри этом прибыль предпри€ти€ с учетом округлени€ до целых единиц продукта составит:
= 787 Ц целых единиц продукта 2-го вида. ѕри этом прибыль предпри€ти€ с учетом округлени€ до целых единиц продукта составит: 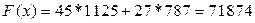 условных единиц (у.е.). ≈сли учитывать дробную часть продукта, то
условных единиц (у.е.). ≈сли учитывать дробную часть продукта, то  (у.е.).
(у.е.).
“аблица 3. “ретий план решени€ задачи (треть€ симплекс-таблица)
| Cj | Ѕазис. пер. | ѕлан | ’1 | ’2 | ’3 | ’4 | ’5 |
| ’1 | 0,5 | -0,25 | |||||
| ’2 | 787,5 | -0,75 | 0,625 | ||||
| ’5 | 2,1 | -2,55 | |||||
| Zj - Cj | 71887,5 | 2,25 | 5,625 |
Ќедоиспользованный ресурс (остаток) составил ’5 = 2475 единиц сырь€ 3-го вида.
¬ последних трех клетках индексной строки записаны двойственные оценки ресурсов трех видов сырь€:  . —мысл двойственные оценки состоит в том, что при увеличении сырь€ первого вида на одну единицу целева€ функци€ вырастит на 2,25 у.е., при увеличении сырь€ второго вида на одну единицу целева€ функци€ вырастит на 5,625 у.е. Ёти виды сырь€ €вл€ютс€ дефицитными и их нужно приобретать в первую очередь. ƒвойственна€ оценка сырь€ третьего вида равна нулю (
. —мысл двойственные оценки состоит в том, что при увеличении сырь€ первого вида на одну единицу целева€ функци€ вырастит на 2,25 у.е., при увеличении сырь€ второго вида на одну единицу целева€ функци€ вырастит на 5,625 у.е. Ёти виды сырь€ €вл€ютс€ дефицитными и их нужно приобретать в первую очередь. ƒвойственна€ оценка сырь€ третьего вида равна нулю ( ). ѕриобретение этого вида сырь€ не имеет смысла, поскольку имеетс€ недоиспользованный ресурс: ’5 = 2475 единиц сырь€ 3-го вида и его приобретение не даст увеличени€ целевой функции.
). ѕриобретение этого вида сырь€ не имеет смысла, поскольку имеетс€ недоиспользованный ресурс: ’5 = 2475 единиц сырь€ 3-го вида и его приобретение не даст увеличени€ целевой функции.
ƒвойственна€ задача
— каждой пр€мой задачей линейного программировани€, представленной моделью (1.1) Ц (1.3), можно св€зать двойственную или сопр€женную модель. ¬ общем виде индексна€ запись такой двойственной задачи будет иметь вид:

 ; (21.1)
; (21.1)
 ; (21.2)
; (21.2)
 . (21.3)
. (21.3)
 «апишем исходную пр€мую задачу (3.1) Ц (3.5) оптимального планировани€ продуктов:
«апишем исходную пр€мую задачу (3.1) Ц (3.5) оптимального планировани€ продуктов:
 ; (22.1)
; (22.1)
 ; (22.2)
; (22.2)
 ; (22.3)
; (22.3)
 ; (22.4)
; (22.4)
 ,
, 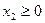 . (22.5)
. (22.5)
 ƒвойственна€ модель по отношению к модели (3.1) Ц (3.5) примет вид:
ƒвойственна€ модель по отношению к модели (3.1) Ц (3.5) примет вид:
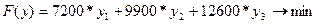 ; (23.1)
; (23.1)
 ; (23.2)
; (23.2)
 ; (23.3)
; (23.3)
 . (23.4)
. (23.4)






