| 334. ѕри виконанн≥ геодезичних вим≥рювань виникають помилки, €к≥ п≥дрозд≥л€ютьс€: | 1. Ќа груб≥ помилки (промахи, простр≥ли) ≥ випадков≥ помилки; 2. “≥льки на систематичн≥ ≥ випадков≥ помилки; 3. Ќа груб≥ помилки, випадков≥ ≥ систематичн≥ помилки. |
| 335. ¬≥д чого залежить виникненн€ тих чи ≥нших помилок при вим≥рах? | 1.Ћише в≥д зовн≥шн≥х природних умов; 2. ¬≥д особи, €ка виконуЇ вим≥рюванн€; 3. ¬≥д приладу, €кий застосовуЇтьс€ при вим≥рах (≥нструментальн≥ помилки0, в≥д особи, що вим≥рюЇ 9особист≥ помилки), в≥д природних умов(помилки зовн≥шн≥х умов). |
| 336. ¬≥д чого залежать груб≥ помилки (промахи, простр≥ли)? | 1. ¬≥д поганих зовн≥шн≥х умов спостереженн€, в≥д поганоњ оптики в ≥нструментах; малий досв≥д роботи ≥ т.д. 2. ¬≥д настрою спостер≥гача при вим≥рах; 3. Ћише в≥д поганоњ методики при вим≥рюванн€х. |
| 337. —истематичн≥ помилки част≥ше всього викишкають в результат≥: | 1. ѕоганих метеоролог≥чних умов при вим≥рах; 2. Ќеуважного ставленн€ до вим≥р≥в виконавц€ роб≥т; 3. ≤снуванн€ помилок в робот≥ приладу (≥нструментальн≥ помилки) Ц не виконувалис€ пов≥рки, обсл≥дуванн€ ≥нструмент≥в. |
| 338. ¬ипадков≥ помилки: | 1. «авжди супроводжуютьс€ одним ≥ тим знаком Ђплюсї, або м≥нусї 2.«авжди бувають грубими по величин≥; 3. ћожуть бути р≥зними по абсолютн≥й величин≥ з р≥зними знаками. |
| 339. ќсновна умова, що характеризуЇ випадков≥ помилки звучить так: ѕри наближенн≥ к≥лькост≥ випадкових помилок до безконечност≥: | 1.—умма њх пр€муЇ до нул€; 2. —ума њх зб≥льшуЇтьс€; 3. —ума њх р≥вна одиниц≥. |
| 340.¬с≥ вим≥рюванн€ в геодез≥њ под≥л€ютьс€ на: | 1. Ћише р≥вноточн≥; 2. Ћише нер≥вноточн≥; 3. –≥вноточн≥ ≥ нер≥вноточн≥. |
| 341. –≥вноточними вим≥рами наз. так≥ вим≥ри, €к≥ виконувались: | 1. Ћише при однакових зовн≥шн≥х умовах; 2. Ћише з використанн€м одного ≥ того ж ≥нструмента; 3. Ћише одним ≥ тим же виконавцем роб≥т, або виконавц€ми з однаковою квал≥ф≥кац≥Їю, ≥ тим же приладом однаков≥ точност≥, при однакових зовн≥шн≥х умовах. |
| 342. Ќер≥вноточними називаютьс€ вим≥ри: | 1. оли вони виконуютьс€ при р≥зних зовн≥шн≥х умовах; 2. оли вони виконуютьс€ одним ≥ тим же спец≥ал≥стом; 3. оли не виконуЇтьс€ хоч одне ≥з сл≥дуючих умов ≥ вим≥ри виконуютьс€ при однакових зовн≥шн≥х умовах, одним ≥ тим виконавцем роб≥т, одним ≥ тим же приладом. |
| 343. оли маЇмо р€д р≥вно точних вим≥р≥в одн≥Їњ ≥ т≥Їњ ж величини ℓ1,ℓ2, ℓ3, ЕЕ..ℓп, то за найб≥льш в≥рог≥дне значенн€ величини що вим≥рюють ≥ приймають: |
1. —ереднЇ арифметичне значенн€, що обчислюЇтьс€ за формулою
Lн.в. =  ,де n Ц к≥льк≥сть вим≥р≥в.
2. —ереднЇ вагове значенн€;
3. јбо середнЇ арифметичне, або середнЇ вагове значенн€ величини, €ку в≥дшукують, вим≥рюють, знаход€ть. ,де n Ц к≥льк≥сть вим≥р≥в.
2. —ереднЇ вагове значенн€;
3. јбо середнЇ арифметичне, або середнЇ вагове значенн€ величини, €ку в≥дшукують, вим≥рюють, знаход€ть.
|
| 344. —ередн€ квадратична похибка окремого вим≥ру при р≥вно точних вим≥рах обчислюЇтьс€ за формулою Ѕесел€, що маЇ такий вигл€д: |
1) m = ±  ;
2) m = ± ;
2) m = ±  ;
3) m = ± ;
3) m = ± 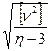 ¬ €ких m - — ѕ, V Ц найб≥льш в≥рог≥дна похибка, n Ц к≥льк≥сть вим≥р≥в, що виконуютьс€.
¬ €ких m - — ѕ, V Ц найб≥льш в≥рог≥дна похибка, n Ц к≥льк≥сть вим≥р≥в, що виконуютьс€.
|
| 345. —ередн€ квадратична похибка середнього арифметичного при р≥вно точних вим≥рах обчислюЇтьс€ за формулою: |
1. ћ = ±  ;
2. ћ = ± ;
2. ћ = ±  ;
3. ћ = m Цn.
де ћ Ц — ѕ середнього арифметичного;
m - — ѕ одного окремого вим≥ру, що обчислюЇтьс€ за формулою Ѕесел€;
n Ц к≥льк≥сть вим≥р≥в. ;
3. ћ = m Цn.
де ћ Ц — ѕ середнього арифметичного;
m - — ѕ одного окремого вим≥ру, що обчислюЇтьс€ за формулою Ѕесел€;
n Ц к≥льк≥сть вим≥р≥в.
|
346. ¬ формул≥ Ѕесел€ п≥д коренем в чисельнику використовуЇтьс€  - сума квадрат≥в найб≥льш в≥рог≥дних помилок при р€д≥ вим≥р≥в. якою вона повинна бути, коли помилки правильно обчислен≥? - сума квадрат≥в найб≥льш в≥рог≥дних помилок при р€д≥ вим≥р≥в. якою вона повинна бути, коли помилки правильно обчислен≥?
|
1.  = 0;
2. = 0;
2.  = m≥n;
3. = m≥n;
3.  = mах; = mах;
|
| 347. Ќайб≥льш в≥рог≥дн≥ помилки при р≥вно точних вим≥рах обчислюють €к р≥зницю кожного окремого з вим≥р≥в ℓn ≥ найб≥льш в≥рог≥дного значенн€ пошукового значенн€ Lн.в. який контроль ≥снуЇ при обчисленн€х суми цих помилок? |
1.  = m≥n;
2. = m≥n;
2.  = 0;
3. = 0;
3.  = mах; = mах;
|
| 348. ћатематична обробка результат≥в р≥вноточних вим≥р≥в виконуЇтьс€ в так≥й посл≥довност≥: | 1.ќбчислюють лише найб≥льш в≥рог≥дне значенн€ вим≥рюваноњ дек≥лька раз≥в величини; 2.ќбчислюють лише найб≥льш в≥рог≥дне значенн€ похибок при вим≥рюванн€х; 3.ќбчислюють найб≥льш в≥рог≥дне значенн€ вим≥р€ноњ величини ≥з р€ду вим≥р≥в ≥ виконують оц≥нку точност≥ результат≥в вим≥рювань. |
| 349. ƒати визначенн€ ваги вим≥ру при нер≥вно точних вим≥рювань в геодез≥њ: | 1. ¬ага Ц це величина обернено пропорц≥йно квадрату — ѕ; 2. ¬ага Ц це величина пр€мо пропорц≥йна квадрату — ѕ; 3. ¬ага Ц це величина р≥вна квадрату — ѕ. |
| 350. ¬ага вим≥ру при нер≥вноточних вим≥рюванн€х обчислюЇтьс€ за формулою: |
1. – =  ;
2. – = m2;
3. – = ;
2. – = m2;
3. – = 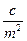 де – вага вим≥ру, n Ц — ѕ вим≥ру, — Ц число любе. де – вага вим≥ру, n Ц — ѕ вим≥ру, — Ц число любе.
|
| 351.¬ формул≥ дл€ обчисленн€ ваги вим≥ру при нер≥вно точних вим≥рюванн€х в чисельнику знаходитьс€ величина — Ц любе число. як його величину вибирають при конкретному р€д≥ вим≥р≥в? | 1. ¬еличина Ђ—ї може бути або р≥вною одиниц≥, або дес€ти, або сотн≥; ќдне з указаних трьох значень вибирають з таким розрахунком, щоб обчислен≥ значенн€ ваги були найб≥льш близькими до одиниц≥; 2.Ѕеруть число, €ке заманетьс€ обчислювачев≥; 3. «авжди беруть р≥вними одиниц≥. |
| 352. ѕри обробц≥ р€ду нер≥вно точних вим≥рювань часто використовують приведен≥ ваги (ваги приведен≥ до одиниц≥). ўо це даЇ? | 1. ÷е даЇ можлив≥сть спростити обчисленн€, практично створити можливими обчисленн€ми усними, без застосуванн€ обчислювальноњ техн≥ки; 2.÷е н≥чого не даЇ; 3.÷е ускладнюЇ процес обчислень. |
| 353. як обчислюЇтьс€ найб≥льш в≥рог≥дне значенн€ вим≥рюваноњ величини при нер≥вно точних вим≥рюванн€х в геодез≥њ? | 1. як середнЇ арифметичне ≥з р€ду нер≥вно точних вим≥р≥в; 2. як середнЇ вагове значенн€ ≥з р€ду вим≥р≥в; 3. јбо €к середнЇ арифметичне, або €к середнЇ вагове ≥з р€ду нер≥вно точних вим≥рювань. |
| 354. ѕри нер≥вно точних вим≥рах, дл€ р€ду нер≥вно точних вим≥р≥в, при оц≥нц≥ точност≥ обчислюють — ѕ одиниц≥ ваги за формулою Ѕесел€. ¬каж≥ть на правильну формулу ≥з трьох приведених нижче: |
1. µ = ±  ;
2. µ = ± ;
2. µ = ±  ;
3. µ = ± ;
3. µ = ±  , де µ - — ѕ одиниц≥ ваги, , де µ - — ѕ одиниц≥ ваги,  - к≥льк≥сть вим≥р≥в,
– Ц вага вим≥р≥в. - к≥льк≥сть вим≥р≥в,
– Ц вага вим≥р≥в.
|
| 355.‘ормула дл€ обчисленн€ середньоњ квадратичноњ похибки середнього вагового маЇ вигл€д: |
1. ћ = µ,
2.ћ =  ,
3. ћ = ,
3. ћ =  ,
де ћ Ц — ѕ середнього вагового значенн€; µ - — ѕ одиниц≥ вага; ,
де ћ Ц — ѕ середнього вагового значенн€; µ - — ѕ одиниц≥ вага;
 - вага вим≥ру. - вага вим≥ру.
|
| 356. ѕри обчисленн≥ найб≥льш в≥рог≥дного визначенн€ величини ≥з р€ду нер≥вно точних вим≥р≥в необх≥дно впевнитис€ в правильност≥ обчисленн€ цього значенн€. ƒл€ контролю обчислюють найб≥льш в≥рог≥дн≥ похибки, €к р≥зницю м≥ж кожним значенн€м вим≥ру ≥ в≥рог≥дним значенн€м. яка ≥з приведених нижче формул використовуЇтьс€ дл€ контролю? |
1.  = 0;
2. = 0;
2.  = 0;
3. = 0;
3.  = m≥n,
де = m≥n,
де  - найб≥льш в≥рог≥дн≥ похибки, - найб≥льш в≥рог≥дн≥ похибки,
 - вага вим≥р≥в. - вага вим≥р≥в.
|
| 357. ќбробка результат≥в р€ду нер≥вно точних вим≥р≥в виконуЇтьс€ таким чином: | 1. ќбчислюють найб≥льш в≥рог≥дне значенн€ вим≥рювальноњ величини, €к середнЇ вагове ≥з р€ду нер≥вно точних вим≥р≥в.; 2. ¬иконують лише оц≥нку точност≥ результат≥в вим≥р≥в; 3. —початку знаход€ть найб≥льш в≥рог≥дне значенн€ вишукуваноњ величини, €к середнього вагового ≥з р€ду нер≥вно точних результат≥в вим≥рювань. |
|
|
|
|
|
|
√еодез≥€.






