Df 6. Бесконечное числовое множество называется счетным, если 
, т.е. существует биекция 
на 
.
Существует биекция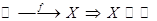 
, т.е. X – счетно. Если множество X счетно, то все элементы можно расположить в некотором порядке 
, 
, соответственно 
.
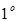Любое непустое подмножество счетного множества либо конечно, либо счетно
Док-во:
Пусть 
- счетно (т.е. 
), тогда его элементы можно расположить в последовательность, т.е.
………………………………….(1)
И пусть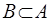 
, 
, 
- первый элемент последовательности (1), является элементом B, так, что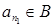 
. Пусть 
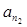- второй такой элемент последовательности (1) так что 
и 
и т.д.
Возможны 2 варианта:
1) «пройдем» по всем элементам множества А и на конечном шаге оборвем этот процесс, в этом случае множество В – конечно.
2) Когда процесс выбора бесконечен получаем бесконечную последовательность 
; 
, при 
, состоящую из всех элементов множества И. положим 
. Отображение 
есть биекция на В, поэтому 
(равномощно), т.е. в случае 2) множество В – счетно.
Следствие. Любое бесконечное подмножество счетного множества счетно.
Df 7. Множество 
называется не более чем счетным, если оно конечно или счетно.
Объединение счетного числа счетных множеств есть множество счетное.
Док-во:
Пусть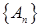 
, (
) – семейство счетных множеств и 
. Расположим каждое множество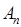 
в последовательность 
………………………………………..
Th 2. Множество всех целых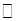 
или рациональных 
чисел – счетное.
Док-во:
1) надо найти биекцию из в 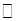, получаем:
Геометрически:
|
|
Следовательно, 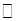- счетно.
2) Рассмотрим 
. поскольку 
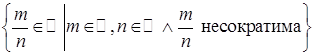. Рассмотрим множество 
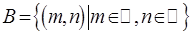, где В – множество всевозможных упорядоченных пар 
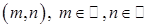. Очевидно 
по Df.
Докажем счетность множества В, для чего построим таблицу:
…………………………………………………………
В этой таблице содержатся все элементы множества В и каждый элемент из В входит в таблицу только один раз. Пронумеровав таблицу согласно стрелкам, получим биекцию на В.
Итак, В – счетно, следовательно 
, тоже счетно.
Th. Всякое бесконечное подмножество счетного множества счетно.
Th 3. Множество 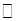на 
несчетно.
Док-во (от противного)
Пусть 
и предположим, что 
- счетное, тогда 
Разделим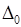 
на три части:
Тогда найдется отрезок, который не содержит 
и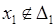 
, 
- делим на 3 части, и выбираем ту из них, которая не содержит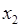 
, т.е. 
и 
, но тогда 
.
Поступаем аналогично с 
Обозначим через 
, ту из равных частей отрезка 
на которой не лежит точка 
. На n -ом шаге получаем, что 
и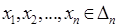 
.
Рассмотрим 
. Согласно th о вложенных отрезках множество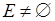 
, т.е. 
, что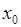 
принадлежит всем отрезкам 
, 
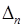, . Итак, на 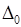, который не совпадает ни с одним 
, .
Получили противоречие, т.к. по предположению 
, т.е. все 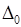состоит из этих точек. Следовательно, предположение не верно.
Th. Множество всех действительных чисел 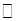несчетно.
Th. Множество всех многочленов 
с рациональными коэффициентами счетно.
Глава II
