| Название предприятий | Стоимость основных фондов, млн. руб. (х) | Выпуск продукции, млн. руб. (у) | ху | 
| 
|
| А | |||||
| 1 ООО «Слава» | 2,4 | 14,4 | 2,692 | ||
| 2 ООО «Лидер» | 4,0 | 32,0 | 3,537 | ||
| 3 ООО «Олимп» | 3,6 | 32,4 | 3,958 | ||
| 4 ООО «СОМ» | 4,0 | 40,0 | 4,380 | ||
| 5 ООО «Сюзи» | 4,5 | 45,0 | 4,380 | ||
| 6 ООО «Престиж» | 4,6 | 50,6 | 4,802 | ||
| 7 ООО «Тандем» | 5,6 | 67,2 | 5,224 | ||
| 8 ООО «Рубин» | 6,5 | 84,5 | 5,646 | ||
| 9 ООО «Злата» | 7,0 | 98,0 | 6,068 | ||
| 10 ООО «Вернисаж» | 5,0 | 75,0 | 6,490 | ||
| Итого | 47,2 | 539,1 | 47,177 |
Чтобы установить, насколько повышается в среднем выпуск продукции при увеличении основных фондов на 1 млн. руб., прежде всего, определим форму связи.
Допустим, что между стоимостью основных фондов и выпуском продукции существует прямолинейная связь, которая выражается уравнением прямой 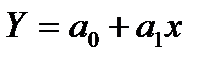 . Параметры уравнения определим при помощи системы двух нормальных уравнений, отвечающих требованию способа наименьших квадратов.
. Параметры уравнения определим при помощи системы двух нормальных уравнений, отвечающих требованию способа наименьших квадратов.


Решим систему нормальных уравнений, для чего каждый член обоих уравнений поделим на коэффициенты при  и из второго уравнения вычтем первое:
и из второго уравнения вычтем первое:

Определим параметр  :
: 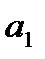 = 0,27 / 0,64 = 0,422.
= 0,27 / 0,64 = 0,422.
Подставим значение  в первое уравнение и найдём параметр
в первое уравнение и найдём параметр  : 4,72 =
: 4,72 =  + 10,8 ∙ 0,422, откуда
+ 10,8 ∙ 0,422, откуда  = 4,72 – 4,56 = 0,16.
= 4,72 – 4,56 = 0,16.
Линейное уравнение корреляционной связи будет иметь следующий вид:  . Параметр
. Параметр  показывает, что с увеличением стоимости основных фондов в среднем на 1 млн. руб. выпуск продукции увеличивается в среднем на 0,422 млн. руб. Параметр
показывает, что с увеличением стоимости основных фондов в среднем на 1 млн. руб. выпуск продукции увеличивается в среднем на 0,422 млн. руб. Параметр  - свободный член уравнения,
- свободный член уравнения, 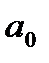 = 0,16, когда х = 0.
= 0,16, когда х = 0.
Подставляем значения параметров  и
и  в уравнение прямой
в уравнение прямой  и находим теоретические, выровненные значения
и находим теоретические, выровненные значения 
 ,
,
 и т.д. (см. табл. 3.4 графа 5).
и т.д. (см. табл. 3.4 графа 5).
Графически зависимость выпуска продукции от стоимости основных фондов показана на рис. 3.3
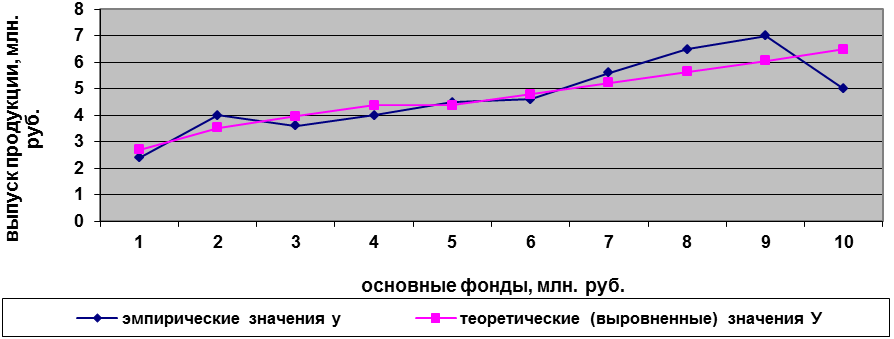
Рис. 3.3 Зависимость выпуска продукции от стоимости основных фондов по 10 предприятиям
Если в результате качественного анализа установлена криволинейная зависимость, принимающая форму кривой второго порядка, то связь выражается уравнением кривой  . Задача сводится к нахождению параметров
. Задача сводится к нахождению параметров  ,
,  и
и  . Для этого необходимо решить систему нормальных уравнений:
. Для этого необходимо решить систему нормальных уравнений:

Пример. Имеются данные о возрасте и выработке по группе рабочих предприятия «А».
| Возраст, лет (х) | 18-22 | 23-27 | 28-32 | 33-37 | 38-42 | 43-47 | 48-52 | 53-50 |
| Выработка деталей на 1-го рабочего, шт. |
Для решения системы нормальных уравнений составим расчётную таблицу (табл. 3.5).
Таблица 3.5
Определение зависимости выработки рабочих предприятия «А» от возраста
| х | у | ху | 
| 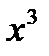
| 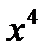
| 
| 
|
| 5,690 | |||||||
| 6,600 | |||||||
| 7,225 | |||||||
| 7,565 | |||||||
| 7,620 | |||||||
| 7,390 | |||||||
| 6,875 | |||||||
| 6,075 | |||||||
| Итого 300 | 55,04 |
Подставим данные таблицы в систему нормальных уравнений:

Поделим каждый член уравнения на коэффициенты при  и получим следующее уравнение:
и получим следующее уравнение:

Вычтем из второго уравнения первое, из третьего – второе и поделим каждый член уравнений на коэффициент при  :
:



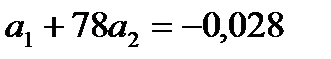
Вычтем теперь из второго уравнения первое и получим:
- 0,017
 , откуда
, откуда 
Подставим в уравнение значение:
 откуда
откуда  = 0,4275 + 0,011 = 0,4385.
= 0,4275 + 0,011 = 0,4385.
Методом подстановки получаем значение  :
:
 ;
;
 откуда
откуда  = - 0,8.
= - 0,8.
Теперь можно записать уравнение параболы:

Отрицательное значение  показывает, что после определённого возраста (в данном случае 43 – 47 лент) выработка рабочих начинает снижаться.
показывает, что после определённого возраста (в данном случае 43 – 47 лент) выработка рабочих начинает снижаться.
Определим теоретические (выровненные) значения  для чего в уравнение кривой подставим значения х:
для чего в уравнение кривой подставим значения х:

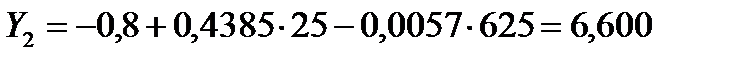 и т.д. (см табл. 3.5 графа 8).
и т.д. (см табл. 3.5 графа 8).
Графически зависимость выработки деталей от возраста рабочих представлена на рис. 3.4.

Рис. 3.4 Зависимость выработки деталей от возраста рабочих предприятия «А»
Другая важнейшая задача - измерение тесноты зависимости - для всех форм связи может быть решена при помощи вычисления эмпирического корреляционного отношения  :
:
 , (3.91)
, (3.91)
где - 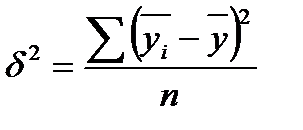 дисперсия в ряду выровненных значений результативного показателя
дисперсия в ряду выровненных значений результативного показателя  ;
;
 - дисперсия в ряду фактических значений у.
- дисперсия в ряду фактических значений у.
Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчёта которого можно использовать следующие формулы:
 , (3.92)
, (3.92)
 , (3.93)
, (3.93)
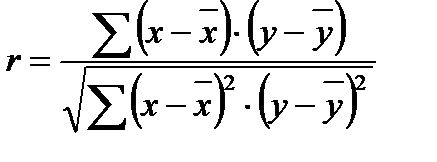 , (3.94)
, (3.94)
 , (3.95)
, (3.95)
Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости.
Пример. Рассмотрим вычисление коэффициента корреляции по стоимости основных фондов и выпуску продукции по 10 предприятиям (табл. 3.6).
Таблица 3.6






