ВЫВОД РАСЧЕТНОЙ ФОРМУЛЫ
Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси О, не проходящей через центр масстела точку С (рис. 2.1).
Если маятник выведен из положения равновесия на некоторый угол j, то составляющая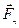 
силы тяжести 
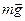уравновешивается силой реакции оси О, а составляющая 
стремится возвратить маятник в положение равновесия. Все силы приложены к центру масс тела. При этом
. (2.1)
Знак минус означает, что угловое смещение j и возвращающая сила имеют противоположные направления. При достаточно малых углах отклонения маятника из положения равновесия sinj» j, поэтому Ft» -mgj. Поскольку маятник в процессе колебаний совершает вращательное движение относительно оси О, то оно может быть описано основным законом динамики вращательного движения
, (2.2)
где М – момент силы Ft относительно оси О, I – момент инерции маятника относительно оси О, 
– угловое ускорение маятника.
Момент силы в данном случае равен
M = Ft×l = – mgj×l, (2.3)
где l – расстояние между точкой подвеса и центром масс маятника.
С учетом (2.2) уравнение (2.3) можно записать
(2.4)
или
, (2.5)
где 
.
Решением дифференциального уравнения (2.5) является функция, позволяющая определить положение маятника в любой момент времени t,
j=j0×cos(w0t+a0). (2.6)
Из выражения (2.6) следует, что при малых колебаниях физический маятник совершает гармонические колебания с амплитудой колебаний j0, циклической частотой 
, начальной фазой a0 и периодом, определяемым по формуле
, (2.7)
где L=I/(mg) – приведенная длина физического маятника, т. е. длина такого математического маятника, период которого совпадает с периодом физического маятника. Формула (2.7) позволяет определить момент инерции твердого тела относительно любой оси, если измерен период колебаний этого тела относительно этой оси. Если физический маятник имеет правильную геометрическую форму и его масса равномерно распределена по всему объему, в формулу (2.7) можно подставить соответствующее выражение для момента инерции (Приложение 1).
В эксперименте исследуется физический маятник, называемый оборотным и представляющий собой тело, колеблющееся вокруг осей, расположенных на разном расстоянии от центра тяжести тела.
Оборотный маятник состоит из металлического стержня, на котором неподвижно укреплены опорные призмы О1 и О2 и две подвижные чечевицы А и B, которые могут закрепляться в определённом положении с помощью винтов (рис. 2.2).
Физический маятник совершает гармонические колебания при малых углах отклонения от положения равновесия 
. Период таких колебаний определяется соотношением (2.7)
,
где I – момент инерции маятника относительно оси вращения, m – масса маятника, d – расстояние от точки подвеса до центра масс, g – ускорение силы тяжести.
Применяемый в работе физический маятник имеет две опорные призмы О1 и О2 для подвешивания. Такой маятник называется оборотным.
Сначала маятник подвешивают на кронштейн опорной призмой О1 и определяют период колебаний Т1 относительно этой оси:
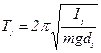(2.8)
Затем маятник подвешивают призмой О2 и определяют Т2:
. (2.9)
Таким образом, моменты инерции I1 и I2 относительно осей, проходящих через опорные призмы О1 и О2, будут соответственно равны 
и 
. Масса маятника m и периоды колебаний Т1 и Т2 могут быть измерены с высокой степенью точности.
По теореме Штейнера
, (2.10)
, (2.11)
где I0 – момент инерции маятника относительно оси, проходящей через центр тяжести. Таким образом, момент инерции I0 можно определить,зная моменты инерции I1 и I2.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Снимите маятник с кронштейна, поместите его на трёхгранную призму так, чтобы расстояния от опоры до призм О1 и О2 не были равны между собой. Передвигая чечевицу вдоль стержня, установите маятник в положение равновесия, после чего закрепите чечевицу винтом.
2. Измерьте расстояние d1 от точки равновесия (центр масс С) до призмы О1 и d2 – от С до призмы О2.
3. Подвесив маятник опорной призмой О1, определите период колебаний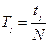 
, где N – число колебаний (не более 50).
4. Аналогичным образом определите период колебаний Т2 относительно оси, проходящей через ребро призмы О2.
5. Подсчитайте моменты инерции I1 и I2 относительно осей, проходящих через опорные призмы О1 и О2, по формулам и , измерив массу маятника m и периоды колебаний Т1 и Т2. Из формул (2.10) и (2.11) определите момент инерции маятника относительно оси, проходящей через центр тяжести (масс) I0. Из двух опытов найдите среднее < I0 >.
6. Передвинув чечевицу А и найдя новое положение центра тяжести С, повторите опыт. Результаты измерений и вычислений занесите в таблицу (см. образец, табл.1).
Таблица 1
| № |
м
|
м
| Ось О1 | Ось О2 |
кг·м2
| ||||||
с
|  ,
с
| 
кг·м2
| 
кг·м2
|
с
|  ,
с
| 
кг·м2
|
кг·м2
| ||||
