Процес первісного запуску підприємства при надходженні інвестиційного потоку описується рівнянням:
 ,
| (17) |
де D – вхідний потік інвестицій; Т – вихідний товарний потік; ф – час;
С – коефіцієнт інерційності системи.
Початкові умови - з розумінь початкового простою підприємства – нульові.
Рівняння (17) є звичайним диференціальним рівнянням першого порядку, що має розв’язок:
 .
| (18) |
Додаткові припущення: підприємство – монополіст, уся продукція споживається, рух товару від виробника до споживача не відчуває ніякого опору. Перевірка отриманого розв’язку на стійкість показує, що система має невласну стійкість:
 .
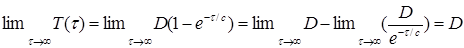| (19) |
Коефіцієнт С характеризує інерційність підприємства стосовно розглянутого процесу. Оскільки в його вираз не входять ніякі зовнішні показники, можна заключити, що він є власною характеристикою підприємства, зумовленою його організаційно-економічним механізмом. Дослідження коефіцієнта інерційності підприємства є окремим завданням і не входить у рамки проведеного дослідження.
Розклад експоненціальної функції в ряд Тейлора показує, що на початковому етапі залежність (18) може бути апроксимована лінійною функцією:
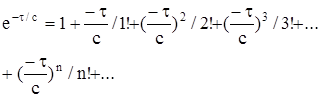
| (21) |
До певного моменту часу ф1 графіки функції (18) та її лінійної апроксимації Тл практично збігаються, однак далі при
| ф > ф1 | (22) |
починається розбіжність функцій Т(ф) і Тл(ф), що різко збільшується згодом. При цьому завжди виконується умова: Тл(ф) ³Т(t), тобто лінійна апроксимація дає завищені результати.
На основі проведеного аналізу можна зробити такі практично важливі висновки:
1. Лінійна апроксимація товарно-часової залежності не припустима в моменти часу, що істотно відрізняються від початкового.
2. При розробці проекту необхідна обов'язкова перевірка на відповідність граничної та проектної величин товарного потоку:
Тпр  .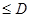
| (23) |
3. Величина С, що характеризує інерційність підприємства стосовно розглянутого процесу, може бути оцінена шляхом дрібних (спробних) інвестицій, за результатами яких можна оцінити доцільність проекту в цілому.
Результати чисельного експерименту показують, що величина опору істотно впливає як на стаціонарне, так і на перехідне значення товарного потоку. Практично важливий висновок, який випливає з цього – необхідність перевірки при розробці бізнес-планів на виконання умови (у випадку наявності опору рухові товарного потоку):
 ,
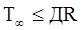| (24) |
де R – коефіцієнт опору руху товарного потоку.
Вплив величини інвестицій Д на характер товарно-часової залежності (рис.3).
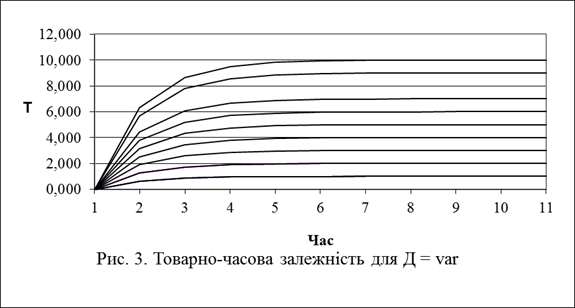
Результати чисельного експерименту показують, що певне перехідне значення товарного потоку буде швидше досягнуто для більшої величини потоку ресурсів Д.
Також було проведено чисельний експеримент для різних значень коефіцієнта інерційності С = var, який показав, що чим більша величина коефіцієнта інерційності, тим за більший проміжок часу буде досягнута проектна потужність. Випадки, коли перехідні процеси в економічній системі супроводжуються запізненням, потребують окремої уваги, тому вони розглянуті окремо. Найпростіший випадок, коли всі процеси, що змінюються у часі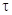 
, затримуються на якусь однакову певну величину затримки Тз , можна описати введенням нового виміру часу:
 .
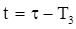| (25) |
Більш складним є випадок, коли час затримки різний для різних концентрованих областей:
| T3i = var. | (26) |
Система рівнянь для трьох концентрованих областей набуває вигляду:
 
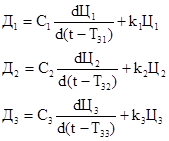
| (27) |
Початкові умови – для кожного рівняння свої:
| t - T3i =0 Þ Цi (T-T3i) = Цi0. | (28) |
При використанні інтегрального перетворення Лапласа для розв’язання системи (27) застосуємо другу теорему зміщення аргументу у вигляді
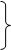 f(t-a) при t > a ³ 0 → e-asF(s)
0 при t < 0
| (29) |
Перехід до простору оригіналів дає:
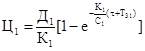
| (30) |
 .
| (31) |
Ще один цікавий випадок запізнення аргументу пов’язаний із застосуванням інтегралу – згортки
 .
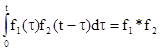| (32) |
Цей інтеграл може бути застосовано, коли протягом часу від 
до 
діють певні фактори f1, кожному з яких відповідає ваговий коефіцієнт f2, що залежить від проміжку часу, який пройшов між моментом t фактора й моментом t нагляду. Сумарний ефект всіх факторів визначатиметься інтегралом (32). Найпростіший економічний приклад такої ситуації – розрахунок інтегральної оцінки певного економічного показника при застосуванні методу експертних оцінок.
Проблема раціоналізації матеріально-грошових потоків – одна з найголовніших проблем життєдіяльності будь-якої фірми. Розгляд цієї проблеми щодо початкового етапу запуску підприємства, тобто при наявності перехідного економічного процесу, показав, що оцінка економії в тих випадках, коли товарно-грошову залежність можна виразити експоненціальною залежністю, описується інтегральним співвідношенням:
 .
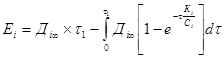| (33) |
Актуальною проблемою сучасної економічної практики є розробка стратегії соціально-економічного розвитку регіонів згідно з розпорядженням Президента України "Про підготовку проекту стратегії економічного і соціального розвитку України на 2002-2011 роки" № 372/2001-рп від 21 грудня 2001 року. Виникає питання щодо застосування наукових наробків до вирішення практичних економічних завдань у зазначеному напрямі. Для моделювання розвитку окремої галузі або промислового об’єднання можуть бути застосовані моделі, побудовані на основі подання економічної системи, що розглядається, ланцюгом послідовних перетворень товарно-грошового потоку. Тобто при розробці стратегії соціально-економічного розвитку регіону можуть бути застосовані такі методичні підходи щодо прогнозування розвитку економічних систем:
- селективний розвиток окремих галузей вивчається за допомогою моделей послідовного перетворення товарно-грошового потоку;
- розвиток регіону як багатогалузевої економічної системи вивчається за допомогою динамічної моделі Леонтьєва.
У тих випадках, коли ми маємо розгалужене виробництво, й нас цікавить собівартість проміжного продукту (для проведення внутрішньозаводських розрахунків тощо) моделі з концентрованими параметрами недостатньо. Потрібна модель з розподіленими параметрами. Прикладом на мікрорівні може бути завдання дослідження собівартості товарного потоку для конвеєрного складання виробів у будь-якій точці конвеєра. Узагальнену схему, яка відображає процес, що моделюється, наведено на рис. 4.
 |
Рис. 4. Схема досліджуваного процесу з розподіленими параметрами
Схема має умовний канал, яким рухається товарно-грошовий потік. Уздовж каналу до потоку надходять необхідні ресурси. Процес описується диференціальним рівнянням:
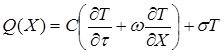. (33)
Кінцевий вираз для поточної собівартості товарно-грошового потоку:
 .
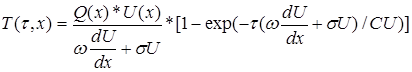| (34) |
Далі розглянемо лагові моделі.
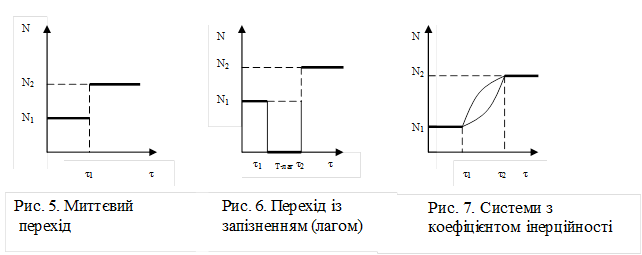На рис. 5 – 7 зображені три можливі варіанти переходу систем від стану з параметрами N1 до стану з параметрами N2.
Перехідний процес у першому наближенні можна описати таким виразом:
| (35) |
де С – коефіцієнт інерційності системи.
Динамічні характеристики економічних систем:
- величина лага Т (для системи з лагом);
- величина часу переходу з режиму з параметрами N1 до режиму з параметрами N2;
- коефіцієнт інерційності С;
- потенційна можливість досягнення потрібного рівня параметрів системи.
Втрати товару:
 .
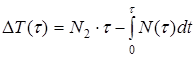| (36) |
