Суспільний поділ праці постійно супроводжує науково-технічний та соціальний прогрес людства. Технічна основа поділу праці - спеціалізація. Але для створення закінченого продукту необхідна узгодженість у роботі та об'єднання спеціалізованих підрозділів й підприємств, тому спеціалізація доповнюється кооперацією. Внаслідок взаємодії цих двох взаємопов'язаних процесів (спеціалізації та кооперації) виробництво матеріальних благ як на мікрорівні (рівень підприємств), так і на макрорівні (рівні галузей промисловості та держави в цілому) являє собою досить довгий ланцюг послідовних перетворень товарного (у загальному випадку товарно-грошового) потоку. Слід зазначити, що на сьогодні актуальні питання математичного моделювання економічних систем, яке б дало змогу не тільки провести дослідження цих систем, а й спрогнозувати їх поведінку. У загальному вигляді таку модель можна відобразити схемою рис. 2.
Рис 2. Загальна послідовність перетворень товарно-грошового потоку
Товарно-грошовий потік, перед тим як потрапити до споживача, проходить n-кінцевих послідовних стадій виробництва, у кожній з яких відбуваються його суттєві перетворення та змінюється ціна. Крім головного товарного потоку, до кожного з об'єктів (стадій виробництва) входять додаткові грошові, енергетичні, трудові, матеріальні, інтелектуальні та інформаційні потоки.
Для нестаціонарного режиму можна записати систему диференціальних рівнянь:
  ,
де Di- вхідні потоки;Сі-коефіцієнти інерційності; Кі- кількість одиниць продукції, Ці- ціна одиниці продукції і-го виду;  -час.
| (1) |
Для замкненості системи рівнянь (1) необхідні початкові умови:
 .
| (2) |
В описаній системі рівнянь не розглядається зміна параметрів протягом безпосередньо стадії переробки, тому цю задачу можна назвати задачею з концентрованими параметрами (областями). З урахуванням нульових початкових умов система (1) приводиться до відомого в літературі виду системи, яка має r лінійно незалежних розв’язків у вигляді:
 
| (3) |
де S0 – дійсний (в загальному випадку комплексний) r – кратний корінь характеристичного багаточлена; Рhk– багаточлен ступеня не вище ніж h-1;h= 1,…,r.
Розроблено ряд моделей, зокрема модель з чотирма концентрованими областями, для якої можна записати систему диференціальних рівнянь
 |
| (4) | |
Для вирішення системи (4) застосовано інтегральні перетворення Лапласа з переходами:  :
| ||
 
| (5) | |
Отримані результати дають можливість записати кінцевий розв'язок системи в просторі Лаплас-образів:
 
 
| (6) |
Зворотний перехід у простір оригіналів дає вираз для першого рівняння:
 .
| (7) |
Розглянемо інші рівняння системи (6). Оскільки кожне з рівнянь являє собою суму двох складових, у випадках, коли другою складовою можна нехтувати, вирази для F2, F3, F4 спрощуються:
 
| (8) |
В цьому разі знаходження оригіналів спрощується:
 
| (9) |
Для з’ясування вимог, за яких зазначене припущення виконується, скористуємось теоремою про кінцеве значення, яка в наших позначках матиме вигляд:
 ,
| (10) |
де і – 1, 2, 3, 4.
Аналіз показує, що для правильності системи приблизних співвідношень (9) повинні виконуватись приблизні рівності:
 .
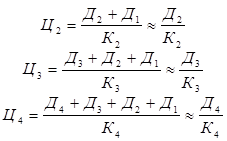| (11) |
Отримана система буде правильною в тому випадку, коли виконується співвідношення
 .
| (12) |
Практично така ситуація може мати місце, коли вартість потоків, що входять до кожної стадії виробництва, значно вища, ніж попередня, тому ціна товарного потоку, що виходить, також значно вища, ніж ціна попереднього. Тобто виконання нерівностей (12) автоматично призводить до нерівностей між цінами
 .
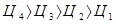| (13) |
За аналогією з виразом (7) можна ввести іншу апроксимацію грошово-часових залежностей типу
 ,
| (14) |
де 
- значення 
.
Відповідно маємо систему кінцевих рівнянь:
 
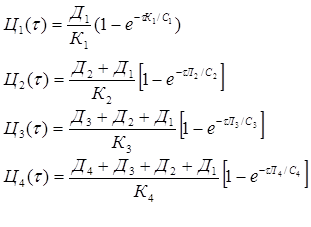
| (15) |
Узагальнюючи отримані вирази (15) на випадок з будь-якою кількістю n концентрованих областей, отримаємо апроксимаційний вираз для будь-якої і-ї області
 .
| (16) |
Однак слід обстежити помилку апроксимації, що являє собою окреме завдання.
Економічною передумовою спрощення моделі (переходу до меншої кількості концентрованих областей) є високий коефіцієнт товарної провідності (що відображає тісні економічні зв'язки) та близькі значення коефіцієнтів інерційності частин. Економічними причинами ускладнення моделі можуть бути погіршення зв'язків між частинами та значні диспропорції коефіцієнтів інерційності.
