ћа€тниковый компенсационный акселерометр на упругом кварцевом подвесе.
÷ель работы: ќзнакомление с принципом действи€ и конструкцией ма€тникового компенсационного акселерометра на упругом кварцевом подвесе (ћ ј), с его основными техническими характеристиками, методикой испытаний и экспериментальное определение масштабного коэффициента и нулевого сигнала акселерометра.
Ќазначение прибора: ма€тниковый компенсационный акселерометр на упругом кварцевом подвесе предназначен дл€ измерени€ проекции кажущегос€ линейного ускорени€ подвижного объекта на ось чувствительности прибора.
—остав лабораторной установки:
Ј √енератор сигналов низкочастотный
Ј ¬ольтметр универсальный
Ј »сточник посто€нного тока с общей точкой
Ј оммутационный блок 1
Ј ќптическа€ делительна€ головка (ќƒ√)
Ј ћа€тниковый компенсационный акселерометр »67-11
“еоретическа€ часть
ѕринцип действи€ акселерометра
јкселерометры примен€ют в системах управлени€ подвижными объектами и в системах навигации, а также в качестве чувствительных элементов системы горизонтальной коррекции гиростабилизаторов.
јкселерометры можно разделить на два типа: гироскопические и негироскопические.
ѕо характеру движени€ инерционной массы различают ма€тниковые акселерометры и акселерометры с линейным перемещением инерционной массы (осевые).
ѕо способу подвеса инерционной массы акселерометры подраздел€ют на п€ть групп:
1. с пружинным подвесом
2. с подвесом в подшипниках скольжени€ или качени€
3. с гидростатическим или гидродинамическим подвесом
4. с газостатическим подвесом
5. с комбинированным подвесом
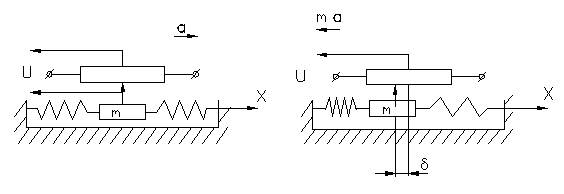
ѕростейша€ схема осевого акселерометра показана на рис.1.„увствительным элементом €вл€етс€ инерционна€ масса m,котора€ может перемещатьс€ относительно корпуса прибора. ѕеремещению массы относительно корпуса противодействуют пружины, прикрепленные одним концом к массе, а другим Ц к корпусу.
ѕри движении корпуса с ускорением a на инерционную массу действует инерционна€ сила ma, котора€ вызывает смещение массы на величину d от исходного положени€. ¬ установившемс€ положении инерционна€ сила уравновешиваетс€ упругой силой, возникающей при деформации пружины:
ma = k пр d, (1)
 |
где kпр - жесткость пружины.
–ис.1.
— потенциометра снимаетс€ напр€жение:
U=kп d, (2)
где kп Ц коэффициент передачи потенциометра.
Ќа основании (1) и (2) получим
U=ka, (3)
где k= kпm/kпр - масштабный коэффициент акселерометра.
‘ормула (3) определ€ет выходную характеристику осевого акселерометра.
 |
–ис.2.
Ќа рис.2. показана кинематическа€ схема ма€тникового акселерометра. ќсь x Ц выходна€, ось zЦ ось чувствительности, ось y составл€ет с ос€ми x и zправую систему координат. ѕри движении основани€ с ускорением a на инерционную массу m действует инерционна€ сила ma. ћа€тниковый момент mal отклон€ет инерционную массу от исходного положени€ (t=0) на угол β. ƒатчик угла (ƒ”) измер€ет угол поворота β, сигнал с ƒ” после усилени€ в усилителе обратной св€зи (”ќ—) поступает на обмотку датчика момента (ƒћ), который создает момент
|
|
|
ћдм=kдм I= kосβ,
где kдм Ц крутизна выходной характеристики ƒћ, [Ќм/ј];
I Ц ток в обмотке ƒћ;
kос=kдуkуосkдм;
где kду - крутизна выходной характеристики ƒ”, [¬/рад];
kуос Ц крутизна выходной характеристики ”ќ—, [A/¬].
¬ установившемс€ положении ма€тниковый момент компенсируетс€ моментом ƒћ:
mlaХcosβ*=kдмI*=kосβ*, (4)
ѕри малых значени€х β cosβ≈1, тогда
mla=kдмI*=kосβ*
—ледовательно,
I*=ka=kgn, (5)
где k=ml/kдм Ц масштабный коэффициент акселерометра,
n=a/g Ц перегрузка, соответствующа€ ускорению a.
‘ормула (5)определ€ет выходную характеристику ма€тникового акселерометра.
”силитель обратной св€зи состоит из усилител€-демодул€тора (”ƒј) и усилител€ компенсации момента (” ћ). —игнал с эталонного сопротивлени€ Rэ поступает в преобразователь ток-частота (ѕ“„).
”равнение движени€ ћ ј.
–ассмотрим рис.3.
ќси xo, yo, zo св€заны с основанием.
ayo, azo Ц составл€ющие ускорени€ основани€ в направлени€х yo, zo;
 xoЦ угловое ускорение основани€ вокруг оси xo.
xoЦ угловое ускорение основани€ вокруг оси xo.
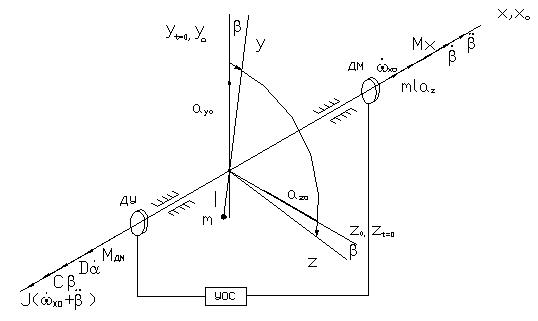 |
–ис.3.
¬ исходном положении акселерометра (t=0), ось yt=0 совпадает с осью yo, а ось zt=0 Ц с осью zo.
ѕри β≠0 ускорение в направлении оси чувствительности
az=azocosβ-ayosinβ
ѕри малом значении угла β cosβ≈1; sinβ≈β, тогда
az=azo-ayoβ (6)
¬округ выходной оси x действуют следующие моменты:
Ј инерционный J( xo+
xo+  ), где J Ц момент инерции подвижных элементов акселерометра вокруг оси x;
), где J Ц момент инерции подвижных элементов акселерометра вокруг оси x;
Ј ма€тниковый момент mlaz;
Ј момент, создаваемый ƒћ по сигналу обратной св€зи;
Ј возмущающий момент ћx;
Ј демпфирующий момент D  , где D Ц удельный демпфирующий момент;
, где D Ц удельный демпфирующий момент;
Ј упругий момент подвеса инерционной массы Cβ, где — Ц углова€ жесткость подвеса.
»спользу€ принцип ƒТјламбера:  =0, получим уравнение движени€ ћ ј:
=0, получим уравнение движени€ ћ ј:
J( xo+
xo+  )+D
)+D  +Cβ+Mдм=mlaz+Mx (7)
+Cβ+Mдм=mlaz+Mx (7)
”читыва€ (6) и выражение ћдм=kосβ, получим:

J  +D
+D  +Cβ+kосβ=mlazo-mlayoβ-J
+Cβ+kосβ=mlazo-mlayoβ-J  xo+Mx
xo+Mx  (8)
(8)
ћоменты mlayoβ, J  xo, Mx вызывает погрешности акселерометра (рассмотрим в п.1.3.)
xo, Mx вызывает погрешности акселерометра (рассмотрим в п.1.3.)
ѕусть ayo=0;  xo=0; Mx=0, тогда уравнение (7) получает вид:
xo=0; Mx=0, тогда уравнение (7) получает вид:

J  +D
+D  +Cβ+kосβ=mlazo (9)
+Cβ+kосβ=mlazo (9)
«апишем уравнение (9) в операторной форме при —<< kос :
(JS≠2+DSβ+C)β(S)+kос(S)β(S) = mlazo(S),
где koc(S)=kду  ,
,
Wк(S)=  - передаточна€ функци€ корректирующих звеньев.
- передаточна€ функци€ корректирующих звеньев.
“ƒћ,“”ƒј,“” ћ Ц посто€нные времени ƒћ,”ƒј,” ћ соответственно.
 |
—труктурна€ схема ћ ј имеет вид (рис.4.):
–ис. 4.
ѕередаточна€ функци€ разомкнутой в точке 1 системы:
W(S)=  =Wо(S)kос(S),
=Wо(S)kос(S),
где Wo(S)=  - передаточна€ функци€ механической части ћ ј.
- передаточна€ функци€ механической части ћ ј.
ѕри параметрах механической части ћ ј типа »67-11:
|
|
|
J=0.47Ј10-4 гсЈсмЈс2
D=0.4 гсЈмЈс
—=0,5 гсЈсм/рад
корни квадратного трехчлена равны:
w1 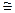 0;
0;
w2 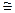 -
-  .
.
“огда
Wo(S)=  =
=  =
=  = =
= =  =
=  =
=  =
=  , где
, где
“м=J/D=1.175Ј10≠≠≠≠≠≠≠≠≠≠≠≠≠-4с.
—ледовательно,
W(S)= 
 (10)
(10)
где kос=kудаkдуkукмkдм
kду=1.547Ј103 пф/рад (в »67-11 используетс€ ƒ” емкостного типа)
kуда=0,3 ¬/пф
kукм=8 ј/¬
kдм=33 гсЈсм/ј
kос=1,23Ј106 гсЈсм/рад
kос/D 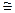 3.075Ј106 гсЈсмЈс
3.075Ј106 гсЈсмЈс
“1=2,3 с
“2=0,0023 с
“3=4Ј10-5 с
“дм=2Ј10-5 с
“уда=4Ј10-5 с
“ укм=2Ј10-5 с
“м=1,175Ј10≠-4≠с
20lg(Koc/D)=129,86.
 |
Ќа рис.5. представлена Ћј‘„’ разомкнутой системы:
–ис.5.
»з графиков рис.5. следует, что ћ ј типа »67-11 €вл€етс€ устойчивой системой с запасом устойчивости по амплитуде m=14.8 дЅ, по фазе γ = 49 град. и частотой среза wср=2118 1/с.
ћаксимальный угол прокачки ма€тника в ћ ј »67-11 не превышает 5 дуг.мин.
ѕри максимальном токе на выходе ” ћ Imax=30 мј в установившемс€ режиме:
kдмI*max=kосβmax,
—ледовательно,
βmax=  дуг.мин.=0,173 дуг.сек.<<5 дуг.мин.
дуг.мин.=0,173 дуг.сек.<<5 дуг.мин.
ѕри значении масштабного коэффициента k=0.25  из (5) получим при I*max =30мј, amax= I*max /k=120 м/c2
из (5) получим при I*max =30мј, amax= I*max /k=120 м/c2 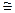 12g.
12g.
ѕогрешности ћ ј
ћетодические погрешности.
ћетодические погрешности ћ ј обусловлены угловым ускорением  xo основани€ вокруг оси xo, совпадающей с осью x ћ ј, и линейным ускорением ayo основани€ (это ускорение называетс€ перекрестным).
xo основани€ вокруг оси xo, совпадающей с осью x ћ ј, и линейным ускорением ayo основани€ (это ускорение называетс€ перекрестным).
»з (8) при Mx=0 получаем:
J  +D
+D  + (C+koc)β=mlazo -J
+ (C+koc)β=mlazo -J  xo-mlayoβ,
xo-mlayoβ,
где с<<koc (c=0.5 гсЈсм/рад; koc=1.23Ј106 гсЈсм/рад).
a)  xo=const; ayo=0;
xo=const; ayo=0;
¬ установившемс€ режиме ( =
=  =0)
=0)



 xo . (11)
xo . (11)
ƒл€ уменьшени€ этой погрешности следует увеличивать koc.
б)  xo=0; ауо=const; azo=const
xo=0; ауо=const; azo=const
B установившемс€ режиме

ќтносительна€ погрешность, вносима€ перекрестным ускорением,
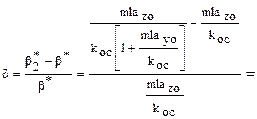
 , (12)
, (12)
где 
≈сли  mlayo/koc<<1, то
mlayo/koc<<1, то 
ƒл€ уменьшени€ этой погрешности следует увеличивать koc и уменьшать ма€тниковость, следовательно, согласно (5) уменьшать масштабный коэффициент ћ ј.
ѕри линейной вибрации основани€
 ;
;
 ,
,
где (ауо)м, (аzo)м Ц амплитуда вибрационного ускорени€ в направлени€х yo , zo соответственно.
ω Ц частота вибрации,
l- фазовый сдвиг,
инерционна€ масса ћ ј совершает вынужденные колебани€, измен€ющиес€ по гармоническому закону:
β=βмsin(ωt+λb),
где βм=  ,
,
A=  - коэффициент динамичности ћ ј
- коэффициент динамичности ћ ј


 - частота собственных незатухающих колебаний.
- частота собственных незатухающих колебаний.
 - относительный коэффициент демпфировани€
- относительный коэффициент демпфировани€

ѕри koc=1.23Ј106 гсЈсм/рад и D=0.4 гсЈсмЈс, J=0.4710-4гсЈсмЈс2 получим:
ω0=5,3Ј103 1/с,
 .
.
ѕри гармонических колебани€х инерционной массы и гармонической вибрации в направлении уо вокруг выходной оси ћ ј по€вл€етс€ посто€нна€ составл€юща€ момента  , равна€
, равна€
0,5ml(ayo)м(β)мcos(l-lb).
ѕогрешность ћ ј при линейной вибрации основани€ равна:
 (13)
(13)
≈сли λ=0, то имеет место Укоса€Ф вибраци€ основани€.
≈сли λ=π/2 и (ауо)м=(azo)м, то имеет место кругова€ вибраци€ основани€.
»з (13) следует, что дл€ уменьшени€ вибрационной погрешности необходимо уменьшать ма€тниковость акселерометра и увеличивать koc.






