1. Алфавіт джерела повідомлення (букви) упорядковують у послідовності спадання їх ймовірності.
2. Одержаний список ділять на дві послідовні частини так, щоб суми ймовірностей букв мало відрізнялися одна від одної. Буквам з першої частини приписується символ 0, а буквам другої частини — символ 1. Аналогічна ситуація з кожною з одержаних частин, якщо вони містять принаймні дві букви.
3. Поділ таким чином триває доти, доки весь список не буде поділено на частини, що містять по одній букві.
4. Після закінчення такого поділу кожній букві (елементу повідомлення) ставиться у відповідність послідовність символів (нулів та одиниць), приписаних у результаті цього процесу для кожної букви.
5. Одержані двійкові послідовності приймають за шукані кодові слова (кодові комбінації)
Приклад. Абстрактний алфавіт з ймовірностями появи його букв у тексті, подано матрицею:
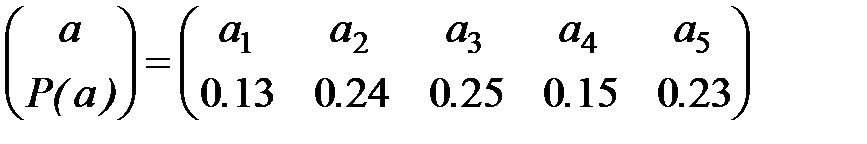
Побудувати відповідний йому код Шенона —Фано.
Процес побудови коду подано у таблиці 6.
| Згідно з даними таблиці одержуємо:
а1 |
| а3 – 0.25 а2 – 0.24 | |||
| а5 – 0.23 а4 – 0.15 а1 – 0.13 | |||
Процес побудови цього коду можна подати в вигляді кодового дерева
| а 3 а 2 а 5 а 4 а 1 |
| Рис 4. |
У даному випадку:
1) ентропія джерела
2) надлишковість джерела
3) середнє число символів в коді
Середнє число символів у коді називають ще коефіцієнтом економічності, або коефіцієнтом ефективності коду.
4) надлишковість коду
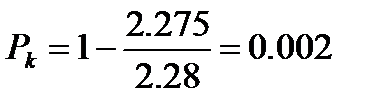
Отже, для коду Шенона—Фано середня кількість двійкових символів, що припадає на символ джерела, наближається до ентропії джерела, але не дорівнює їй.
Цей підтверджений прикладом результат є наслідком теореми кодування без перешкод (шуму) для джерела (першоа теорема Шенона).
Обчислимо за співвідношенням (3.7) значення вектора Крафта
Отже, даний конкретний код є оптимальним.
Зауважимо, що розглянутий метод Шенона—Фано не завжди приводить до побудови однозначного коду. Хоча у верхній підгрупі середня ймовірність символа більша (і тому кодові слова повинні бути коротшими), можливі ситуації, за яких програма зробить довшими коди деяких символів з верхніх підгруп, а не коди символів з нижніх підгруп. Так, поділяючи множину символів на підгрупи, можна зробити більшою по ймовірності як верхню, так і нижню підгрупи.
4. Алгоритм Хаффмена для побудови оптимального коду
Метод побудови оптимального префіксного коду, який завжди дає однозначний результат, запропонував у 1952 році американський учений Девід Хаффмен (1925-1999). Це дуже ефективний спосіб пошуку оптимального вектора Крафта l для вектора частот p, тобто такого l, для якого сума L(m)=(l1*p1+l2*p2+…+lk*pk) є мінімальною. Одержаний з використанням оптимального вектора Крафта l, (коли нерівність (3.7) перетворюється в строгу нерівність) префіксальний код для p є оптимальним кодом Хаффмена.
Алгоритм Хаффмена
1. Виписати в рядок усі символи алфавіту джерела в порядку спадання ймовірностей їх появи в тексті.
2. Послідовно об’єднувати два символи з найменшими ймовірностями в новий символ, ймовірність появи якого як такого, що дорівнює сумі ймовірностей його складових.
3. Вказівку 2 виконувати до тих пір, доки не будуть об’єднані всі символи (із сумою ймовірностей 1).
4. Побудувати кодове дерево, кожний вузол якого має сумарну ймовірність усіх вузлів, розміщених нижче від нього.
5. Простежити шлях до кожної вершини дерева, помічаючи напрям до кожного вузла (ліворуч – 0, праворуч – 1). Одержана послідовність нулів та одиниць дає кодове слово, що відповідає кожному символові алфавіту джерела повідомлень.
Приклад. Побудувати код Хаффмена для джерела повідомлень з алфавітом
= 
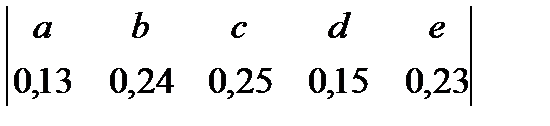
1. Розташовуємо букви алфавіту в порядку спадання їхніх ймовірностей
2. Виконуючи вказівки 2, 3 алгоритму послідовно одержуємо
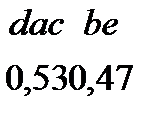
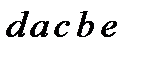
3. За вказівкою 4 будуємо кодове дерево (рис. 5)
Рис. 5
4.
| b |
| e |
| c |
| a |
| d |
Відповідно до вказівки (5) алгоритму одержуємо:
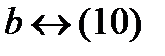
Для обчислення середнього числа символів l, що припадають на одну букву джерела повідомлення скористаємося формулою (3.4)
Ентропію джерела обчислюємо за формулою (3.1)
Отже, 
За співвідношенням (3.7) обчислюємо значення вектора Крафта.
2-3+2-2+2-2+2-3+2-2= 
+ 
Отже, побудований код Хаффмена є близьким дооптимального. Зазначимо, що в деяких випадках результати двійкового кодування за алгоритмами Шенона—Фано та Хаффмена схожі в тому розумінні, до довжини відповідних кодових слів в обох випадках збігаються.
Має місце твердження: Якщо ймовірності джерела є степенями двійки, то довжини відповідних кодових слів У кодах Шенона—Фано і Хаффмена збігаються.
5. Оптимальні нерівномірні коди і проблеми стискування інформації
Стискування даних забезпечує більш ефективне використання ємності дискової пам’яті. Наприклад, для відеоінформації, де відтворення кадра (фрейма) реалізується з швидкістю 30 разів за секунду, необхідне стискування у 100 і більше разів.
Дуже корисним є стискування для передавання інформації в будь-яких системах зв’язку. Стискування інформації в цьому випадку дозволяє передавати значно менші (як правило, в декілька разів) обсяги даних, що вимагає значно менших ресурсів пропускної здатності каналів для передачі тієї ж інформації. Виграш може бути і в скороченні часу завантаження каналу, що приводить до значної економії коштів.
Для характеристики досягнутого ступеня стискування на практиці застосовують так званий коефіцієнт стискування: відношення початкового розміру до розміру в стиснутому вигляді.
Відомі методи стискування спрямовані на зниження надмірності, яка викликана як нерівною апріорною імовірністю символів, так і залежністю між порядком надходження символів. У першому випадку для кодування початкових (вихідних) символів використовують нерівномірні коди.
Усунення надмірності, яка обумовлена кореляцією між символами, засноване на переході від кодування окремих символів до кодування груп цих символів.
Отже, процес усунення надмірності джерела повідомлень зводиться до двох операцій — декореляції (укрупнення алфавіту) й кодування оптимальними нерівномірними кодами.
Усі алгоритми стискування поділяють на дві великі групи: алгоритми з втратами й алгоритми без втрат.
Стискування з втратами дозволяє досягнути значно більшого ступеня стискування (до 
і менше від початкового обсягу). Наприклад, відеофільм, що займає в неупаковому вигляді 30 Гбайт, вдається записати на CD ROM. Але алгоритми стискування з втратами приводять до деяких змін самих даних. Тому застосувати такі алгоритми можна тільки до тих даних, для яких невеликі спотворення не є істотними: відео, фотозображення (алгоритми JPEG), звук (алгоритми МРЗ).
Стискування без втрат є менш ефективним ніж стискування з втратами. Тут ступінь стискування ефективно залежить від конкретних даних. Але дані, стиснуті за методом без втрат, після розпакування цілком ідентичні вихідним, що є абсолютно необхідним для текстових даних, програмного коду.
Більшість алгоритмів стискування без втрат поділяють на дві групи: словникові й статистичні методи.
Словникові методи характеризуються високою швидкістю стискування-розпаковки, але дещо гіршим стискуванням. Ефективні словарні алгоритми стискування інформації розробили ізраїльські вчені Якайба Зіва та Абрахма Лемпеля (алгоритм Lempel Ziv, скорочено LZ) на основі методу словників.
На основі алгоритмів LZ фірми розробники програмного забезпечення створили програмні засоби, які широко використовуються для стискування (компресії) та відновлення (декомпресії) даних, що забезпечує значну економію пам’яті на рухомих носіях (зовнішньої пам’яті).
Статистичні методи — це ймовірнісні методи стискування — алгоритми Шенона—Фано і Хаффмена, які детально розглянуті в п. 3.3 і п. 3.4.
Є два види імовірнісних методів. Їх основною відмінністю є способи визначення появи кожного символу.
1. Статистичні методи, які використовують фіксовану таблицю частоти появи символів.
2. Динамічні, чи адаптивні, методи, в яких частота появи символів весь час змінюється і в міру зчитування блоку даних відбувається перерахунок початкових значень частот.
Статистичні методи характеризуються хорошою швидкодією і не вимагають значних ресурсів пам’яті. Вони широко застосовуються в багаточисленних програмах-архіваторах, наприклад, ARK, PKZIP та інших.
Динамічні методи мають меншу швидкодію і вимагають більших обсягів пам’яті.
Для стискування даних, що передаються модемами, використовують так зване арифметичне кодування ([10, п. 2.4]).
Принципи арифметичного кодування були розроблені наприкінці 70-х років ХХ століття. У результаті арифметичного кодування рядок символів замінюється дійсним числом х (0<х<1). Арифметичне кодування дозволяє забезпечити високий ступінь стискування, особливо в тих випадках, коли стискуються дані, де частота появи різних символів дуже змінюється.
Тема 9. Нерівномірні двійкові первинні коди.
План
1. Класифікація первинних кодів.
2. Код Морзе.
3. Число-імпульсні коди.
