Работа и мощность

Законы сохранения

Законы сохранения в природе

 

В природе имеют место несколько законов сохранения.

Эти законы говорят о том, что при определенных условиях некоторая физическая величина сохраняет свое значение. Существуют законы сохранения энергии, импульса, момента импульса, заряда и др.

Физики часто пользуются законами сохранения по следующим причинам.

Во-первых, законы сохранения не зависят от характера действующих сил и от вида траектории. Поэтому они позволяют получить общие и существенные выводы без решения уравнений движения. Иногда из закона сохранения вытекает, что что-то оказывается невозможным. Например, мы не тратим попусту время на разработку конструкции вечного двигателя.

Во-вторых, законы сохранения могут быть использованы в тех случаях, когда силы неизвестны. Так, в частности, дело обстоит при рассмотрении соударяющихся тел, в физике элементарных частиц и др.

В-третьих, даже в тех случаях, когда силы известны, законы сохранения позволяют существенно облегчить решение задачи. Для решения задачи следует, прежде всего, попытаться применить соответствующий закон сохранения и только после этого переходят к составлению других уравнений.

В этой главе мы рассмотрим законы сохранения механической энергии и импульса. Ограничимся областью малых скоростей движения (v<<c), в которой справедливы преобразования Галилея.

Прежде чем переходить к законам сохранения энергии и импульса, необходимо ввести понятия работы силы, импульса, кинетической и потенциальной энергии.

 

Работа и мощность

Пусть материальная точка, на которую действует сила F, совершает перемещение d r. Действие силы F на участке d r характеризуется работой.

Работой dA, совершаемой силой F на участке d r, называется скалярное произведение силы F на перемещение точки приложения силы d r.

dA = F ×d r = F×dr×cos(F,d r)=F_r×dr, (11.1)

где F_r- проекция силы F на направление d r.

В декартовой системе координат выражение для элементарной работы примет вид:

dA = F ×d r = . (11.2)

Для вычисления работы на протяженном участке 1-2 (рис.11.1), необходимо его мысленно разбить на малые участки d r и на каждом из них вычислить работу dA. Полная работа на участке 1-2 будет равна, очевидно, сумме всех работ dA на этом участке.

. (11.3)

 

Интеграл типа (11.3) в общем случае является криволинейным интегралом, вычисление которого вызывает определенные трудности. Однако в некоторых частных случаях он вычисляется достаточно просто. Например.

а) Работа постоянной силы

В этом случае, вынося постоянную величину F за знак интеграла, получим:

А = (11.4)

Работа постоянной силы равна скалярному произведению силы на перемещение точки приложения силы.

б) точка приложения силы движется прямолинейно

Пустим ось X системы координат вдоль перемещения d r. Тогда выражение (11.2) примет вид: dA = F_xdx.Пусть нам известна зависимость проекции силы F_x от координаты x, график которой представлен на рис 11.2.

В этом случае величина работы имеет геометрическую интерпретацию.

Величина работы dA силы F на участке dx, являющаяся произведением F_xdx, равна площади заштрихованного участка на рис.11.2. Тогда суммарная площадь всех dA равна площади под кривой F_x(x) от x₁ до x₂ () и, соответственно, равна полной работе силы на этом участке.

При прямолинейном перемещении точки приложения силы вдоль оси X работа силы численно равна площади под кривой F_x(x) от x_нач до x_кон.

 

Количество работы, совершаемой силой за единичный отрезок времени, характеризует мощность N силы F.

Мощность N силы F при перемещении d r точки ее приложения за время dt вычисляется по выражению:

. (11.5)

Средняя мощность áNñ силы F за время Dt равна отношению полной работы А силы за это время к промежутку времени Dt.

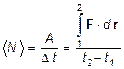. (11.6)

Необходимо отметить, что при определении работы нужно строго следовать формуле (11.2), а не полагаться на интуитивные ощущения.

Дело в том, что понятие работы в физике отличается от житейского понятия работы. Если Вы возьмете стокилограммовую штангу, и будете держать ее на весу, то очень быстро устанете. Вам будет казаться, что Вы совершаете большую «работу», хотя работа мышечных усилий, как ее понимают в физике, равна нулю.

Прежде чем отвечать на вопросы о работе, необходимо уяснить о работе каких сил идет речь, поскольку работу в физике совершают силы, а не предметы и механизмы.

Единицей работы служит работа, совершаемая постоянной силой в 1Н, действующей вдоль перемещения, при перемещении точки ее приложения в 1м. Эта единица называется джоулем.

1Дж = 1Н×м.

Единицей мощности является такая мощность, при которой за одну секунду совершается работа, равная одному джоулю. Такая единица называется ваттом.

1Вт = 1Дж/с = 1Н×м/с.