Технологические задачи прокатного производства.
Технологические задачи в прокатном производстве напоминают по своей направленности и методам решения задачи ковки и штамповки.
Инженеру – технологу приходится решать вопросы расчета формоизменения, чтобы обеспечить изделиям нужную форму и точность; определить силу деформации, необходимую для прокатки, чтобы правильно назначить величину деформации за пропуск или выбрать соответствующий прокатный стан; прокатка сопровождается порой разрушением металла, поэтому приходится решать вопросы об оптимальной технологии прокатки, обеспечивающей соответствующую производительность и качество продукции.
Элементы теории продольной прокатки.
Продольная прокатка полосы может осуществляться только при определенных соотношениях параметров полосы и валков.
Для того, чтобы произошел захват полосы валками, то есть полоса получила определенное ускорение и начала деформироваться, необходимо чтобы в начальный момент соприкосновения полосы и валков силы способствовали продвижению полосы через валки.
 |
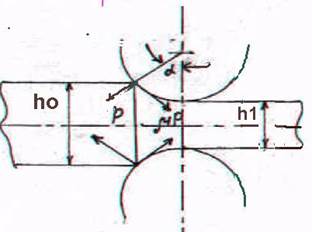Должно выполняться, по крайней мере, условие
или
(2.1)
Здесь обозначено: р – давление на валок; 
– сила трения, принятая по Кулону.
Если воспользоваться определением угла трения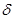 
,
то условие (2.1) примет вид
, (2.1а)
то есть для осуществления захвата необходимо, чтобы угол захвата был меньше угла трения.
Угол захвата 
является одним из важнейших параметров, определяющих производительность прокатки.
Прокатка служит для уменьшения толщины полосы 
. Чем выше допустимый угол захвата , тем большее обжатие можно совершить за один пропуск полосы через валки.
На обжимных станах (блюмингах и слябингах) применяют валки с насеченной, с рифлёной или наваренной поверхностью, что увеличивает угол трения и позволяет иметь на этих станах высокие обжатия
Однако, не во всех случаях возможно применение валков с грубой поверхностью. В чистовых прокатных клетях формируется поверхность готового профиля. Высокие требования предъявляются к качеству поверхности холоднокатаных листов, поэтому приходится применять валки шлифованные, а прокатку вести со смазкой. Углы охвата при этом имеют весьма малую величину (3 - 4 
).
Условие (2.1) или (2.1а) отличается предельной простотой. Однако оно не дает возможности учесть во всей полноте условия, в которых протекает процесс заполнения очага деформации и перехода к установившейся стадии прокатки.
Более полная теория захвата полосы рассматривает условия взаимодействия полосы и валков не только в первоначальный момент их соприкосновения, но и в ходе всего процесса заполнения очага деформации.
При этом особый интерес представляет кинематика взаимодействия полосы и валков, то есть соотношение между скоростями полосы и валков, которым определяются условия трения на поверхности контакта металла с валком.
Помимо кинематических условий на контактной поверхности важную роль в процессе заполнения очага деформации металлом играет характер формоизменения переднего конца полосы при движении его вдоль очага деформации, а также силовые факторы – трение, сопротивление деформации, инерционные усилия. Инерционные силы влияют наибольшим образом в начальный момент захвата.
 |
 |
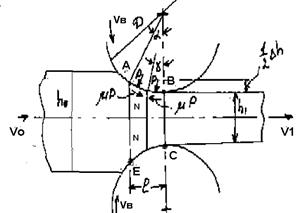Допустим, захват металла произошел. Передний конец полосы, приобретая по толщине размер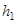 
, вышел из валков. Началась стадия установившейся прокатки. Познакомимся с параметрами геометрического очага деформации ABCЕ. Напишем условие постоянства объема полосы:
= 
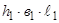
или
(2.2)
Обычно обозначают
; 
; 
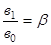Коэффициенты 
, 
соответственно называют относительным обжатием, относительным уширением и относительным удлинением. Иногда 
и 
называют коэффициентом уширения и коэффициентом удлинения.
Коэффициент вытяжки 
за один проход обычно находится в пределах 1.1 – 1.6 и в некоторых специальных случаях доходит до 2.5 – 4.
Иногда деформации полосы выражаются в логарифмическом виде 
, 
. Условие постоянства объёма (2.2) в этом случае можно записать
= 
(2.2а)
Центральный угол можно вычислить по формуле
или
Проекция дуги захвата АВ на направление прокатки носит название длины очага деформации или длины контактной поверхности и вычисляется по формуле
или, пренебрегая величиной 
по сравнению с величиной 
, по приближенной и нашедшей наибольшее распространение формуле
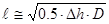(2.4)
Часто вводят понятие о средней ширине и средней высоте очага деформации
(2.5)
Для характеристики геометрических соотношений в очаге деформации применяют безразмерные величины
,
в которых 
и h вычисляют по формулам (2.4) и (2.5).
Рассмотрим соотношение скоростей металла полосы и валков на дуге захвата АВ.
Скорость валка на дуге АВ остается постоянной. Скорость полосы вдоль очага деформации нарастет от 
до 
. Причем в некотором сечении скорости валка и полосы становятся равными друг другу.
 |
Это сечение полосы называется критическим, центральный угол, соответствующий этому сечению, обозначают 
(предыдущий рисунок) и называют критическим (или нейтральным) углом.
Часть дуги АВ, на которой скорость металла меньше скорости валков, называют зоной отставания, вторая часть дуги, где металл движется с большей скоростью, чем валки, называют зоной опережения.
Опережение S характеризуется удельной разностью скорости полосы на выходе и окружной скоростb валков 
и выражается в процентах
(2.6)
Выведем формулу расчета опережения. Опережение – важный кинематический параметр, который, например, учитывается при настройке станов непрерывной прокатки для того, чтобы согласовать скорости вращения валков по клетям.
Сделаем допущение, что скорость металла 
в некотором сечении не зависит от координат У и Z – это так называемая гипотеза плоских сечений.
Будем считать, что на всей дуге АВ (предыдущий рисунок) имеет место скольжение деформируемого металла по поверхности валков, нет зоны прилипания. Эти условия довольно точно соблюдаются при прокатке листов и лент. Далее, будем считать, что справедлив закон трения Кулона.
Напишем условие постоянства расхода для сечения выхода из валков, площадь которого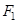 
, и критического сечения 
(предыдущий рисунок)
или
,
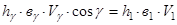где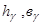 
- высота (толщина) и ширина полосы в нейтральном сечении.
Из последнего соотношения вытекает
Обычно критический угол меньше 
, в зоне опережения полоса получает малое обжатие и ещё меньше отличаются между собой 
и 
.
Итак, если пренебречь уширением, что вполне справедливо при прокатке ленты или листа, то
(2.7)
Обжатие полосы между нейтральным сечением и сечением выхода
,
отсюда высота полосы в нейтральном сечении NN (предыдущий рисунок)
(2.8)
Следовательно, опережение (2.6) с учетом (2.7) и (2.8) можно представить следующей формулой
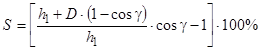(2.9)
Эта формула показывает, что опережение растет с ростом угла , диаметра валков D=2R и уменьшением высоты полосы .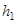
Многочисленные исследования показывают, что качественное и количественное совпадение результатов опыта и расчета по формуле (2.9) можно признать удовлетворительным, если речь идет о прокатке достаточно тонких полос и лент.
В формулу (2.9) входит критический угол. Определим его из условия равновесия сил, действующих в очаге деформации (предпоследний рисунок)
Проектируя все силы, приложенные от валков к прокатываемой полосе, на ось прокатки Х и приравнивая их к нулю, получаем
,
или приняв в первом приближении р=const вдоль дуги АВ
Отсюда после простых преобразований получим
Если углы и малы, то можно принять
и из последнего выражения получим простую приближенную формулу
(2.10)
Из последнего равенства следует, что с ростом коэффициента трения угол и, связанное с ним формулой (2.9) опрежение, возрастают.
Зависимость от имеет экстремум, которому соответствует
Приняв в формуле (2.10) =0, получим значение углов захвата, при которых опережение равно нулю
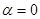и 
Последнее показывает, что после того, как осуществился захват, очаг деформации приобретает большой резерв сил, способствующих прокатке.
Предельный угол в установившейся стадии в два раза больше начального угла захвата. Для увеличения производительности прокатного стана известна рекомендация осуществлять некоторое сближение валков после того, как произошел захват полосы валками. При сближении валков увеличивается угол и растёт обжатие.
