»з приведенных примеров видно, что числа — и D могут быть как положительными, так и отрицательными.ќни могут, в частности, даже обращатьс€ в нуль.
–ассмотрим, однако, наиболее интересный в приложени€х случай, когда ни — ни D нулю не равны.“огда, как нетрудно видеть, точка равновеси€ определ€етс€ парой

Ёти формулы €вл€ютс€ весьма примечательными:в равновеснойситуации выбор игрока ј полностью определ€етс€ элементами платежной матрицы игрока ¬,
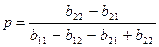
(и не зависит от элементов его собственной платежной матрицы), а выбор игрока ¬ в равновесной ситуации полностью определ€етс€ элементами платежной матрицы игрока ј,

(и не зависит от элементов его собственной платежной матрицы).
»ными словами, равновесна€ ситуаци€ обоих игроков определ€етс€ не столько стремлением увеличить собственный выигрыш, сколько желанием держать под контролем выигрыш другого игрока (минимизировать этот выигрыш). » если, например, заменить в биматричной игре матрицу выплат игроку ј, а матрицу выплат игроку ¬ оставить прежней, то игрок ј никак не изменит своего "равновес≠ного" поведени€ (просто не обратит внимани€ на эту замену), в то врем€ как игрок ¬ изменит свою стратегию на новую, равновесную.
“аким образом, в биматричной (неантагонистической) игре мы вновь встречаемс€ с антагонизмом. ѕравда, теперь это уже не антагонизм интересов (как было в антагонистической, матричной игре), а антагонизм поведени€.
ќтметим, что в биматричных играх (в отличие от матричных) при наличии нескольких ситуаций равновеси€ средний выигрыш игрока в разных равновесных ситуаци€х различен (напомним, что в матричной игре выигрыш игрока один и тот же вне зависимости от количества точек равновеси€).
Ќо если средние выигрыши разн€тс€,токакую равновесную ситуацию следует считать оптимальной?
Ќаконец, еще одно, не менее интересноеобсто€тельство. ¬спомним, с какими трудност€ми мы столкнулись, пыта€сь перевести эмоциональные оценки результатов общени€ студент-преподаватель в количественные показатели. ¬ целом сохран€€ основные соотношени€, эти количественные оценки могут, конечно, измен€тьс€ как от студента к студенту, так и от преподавател€ к преподавателю. ќднако если эти изменени€ будут не слишком значительными Ц элементы платежной матрицы "пошевельнутс€" слегка Ц то слегка "пошевельнутс€" и зигзаги, не измен€€ ни своей общей формы, ни взаимного расположени€, а значит, число равновесных ситуаций не изменитс€. ¬прочем, сказанное относитс€ лишь к случаю, когда множество ситуаций равновеси€ конечно и состоит из нечетного числа точек (одной или трех).
ак прин€то говорить в подобных случа€х, это число устойчиво относительно малых шевелений.
онечно, в некоторых биматричных играх равновесные ситуации случаютс€ и в чистых стратеги€х (в последнем из разобранных примеров таких ситуаций даже две). Ќо, как показывают разобранные примеры, во-первых, чистой ситуации равновеси€ может вовсе не быть, и, во-вторых, даже при ее наличии не исключено существование равновесных ситуаций в смешанных стратеги€х. », чтобы найти их все, неизбежно приходитс€ обращатьс€ к описанному выше подходу.






