«адача 4.1. а) ск≥льки в середньому з≥ткнень за 1 с при нормальних умовах в≥дбуваЇтьс€ в одн≥Їњ молекули азоту, €кщо њњ д≥аметр 3,1-ё"8 см? б) ск≥льки в середньому з≥ткнень одн≥Їњ молекули азоту в≥дбуватиметьс€, €кщо температура п≥двищитьс€ на 273 ∞—?
–≥шенн€. а) середнЇ число з≥ткнень дл€ одн≥Їњ молекули азоту за 1 с при нормальних умовах визначаЇтьс€ за формулою

де  - середн€ арифметична швидк≥сть молекул. “од≥
- середн€ арифметична швидк≥сть молекул. “од≥
формула середнього числа з≥ткнень молекули за 1 с набуде вигл€ду
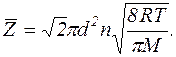
ѕ≥дставл€ючи числов≥ значенн€ величин, вз€тих в одиниц€х системи —≤, знаходимо
 б) €кщо температура азоту п≥двищитьс€, то число молекул в одиниц≥ об'Їму зменшитьс€, оск≥льки зб≥льшитьс€ об'Їм в≥д V0 до V1. онцентрац≥ю молекул азоту при п≥двищенн≥ температури та сталому тиску знаход€ть за р≥вн€нн€м ≥зобарного процесу
б) €кщо температура азоту п≥двищитьс€, то число молекул в одиниц≥ об'Їму зменшитьс€, оск≥льки зб≥льшитьс€ об'Їм в≥д V0 до V1. онцентрац≥ю молекул азоту при п≥двищенн≥ температури та сталому тиску знаход€ть за р≥вн€нн€м ≥зобарного процесу

ќск≥льки число молекул N0 в об'Їмах V0 та V1 не зм≥нилось, то концентрац≥€ молекул n1 при температур≥ “1 буде n1=  , але
, але

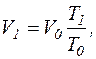
тод≥

—ереднЇ число з≥ткнень молекули азоту за 1 с при даних умовах дор≥внюватиме
 ¬≥дпов≥дь:
¬≥дпов≥дь:  =5,2×109с-1;
=5,2×109с-1;  3,68×109c-1.
3,68×109c-1.
«адача 4.2. ¬изначити середню довжину та тривал≥сть в≥льного проб≥гу молекул кисню при тиску 200 ѕа та температур≥ 27 ∞—, €кщо д≥аметр молекули кисню 2,9×1010 м.
–≥шенн€. якщо середн€ довжина в≥льного проб≥гу молекули  , а њњ середн€ швидк≥сть
, а њњ середн€ швидк≥сть 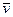 , то число з≥ткнень за 1 с
, то число з≥ткнень за 1 с  , а тривал≥сть в≥льного проб≥гу
, а тривал≥сть в≥льного проб≥гу  “акий самий результат одержимо, €кщо виразимо середню довжину в≥льного проб≥гу
“акий самий результат одержимо, €кщо виразимо середню довжину в≥льного проб≥гу  через середню швидк≥сть та час в≥льного проб≥гу
через середню швидк≥сть та час в≥льного проб≥гу  :
:
 зв≥дки
зв≥дки 
—ередн€ довжина в≥льного проб≥гу дор≥внюЇ

де n - концентрац≥€ молекул.
онцентрац≥ю молекул визначимо з основного р≥вн€нн€: молекул€рно-к≥нетичноњ теор≥њ газ≥в 
«в≥дки

—ередн€ довжина в≥льного проб≥гу дор≥внюватиме

ѕ≥дставл€ючи числов≥ значенн€ величин, вз€тих в одиниц€х системи —≤, знаходимо

—ередн€ арифметична швидк≥сть молекул

Ўуканий середн≥й час в≥льного проб≥гу молекул


ѕ≥дставл€ючи числов≥ значенн€ величин, вз€тих в одиниц€х системи —≤, знаходимо

¬≥дпов≥дь:  = 5,49×10-5 м;
= 5,49×10-5 м;  = 1,23×10-7 с.
= 1,23×10-7 с.
«адача 4.3. ¬изначити середню довжину в≥льного проб≥гу молекул кисню при нормальних умовах, €кщо коеф≥ц≥Їнт в'€зкост≥ 1,92-10 5ѕас.
–≥шенн€. ƒл€ визначенн€ середньоњ довжини в≥льного проб≥гу молекул кисню скористаЇмось формулою, €ка виражаЇ коеф≥ц≥Їнт в'€зкост≥ через довжину в≥льного проб≥гу, середню арифметичну швидк≥сть молекул та густину газу
 , зв≥дки
, зв≥дки 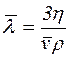 .
.
«ам≥нивши в останн≥й формул≥ швидк≥сть

д≥станемо

ѕ≥дставивши числов≥ значенн€ величин, вз€тих в одиниц€х системи —≤, знаходимо

¬≥дпов≥дь: 
«адача 4.4. ¬изначити коеф≥ц≥Їнти внутр≥шнього терт€ ≥ дифуз≥њ кисню, €кий знаходитьс€ при тиску 0,2 ћѕа ≥ температур≥ 280 .
–≥шенн€. Ќа основ≥ молекул€рно-к≥нетичноњ теор≥њ газ≥в коеф≥ц≥Їнт внутр≥шнього терт€ ≥деального газу (динам≥чна в'€зк≥сть) ≥ коеф≥ц≥Їнт дифуз≥њ визначитьс€ за формулами
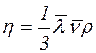 (1)
(1)
 (2)
(2)
де  - густина газу;
- густина газу;
 - середн€ довжина в≥льного проб≥гу молекул;
- середн€ довжина в≥льного проб≥гу молекул;
|
|
|
 - середн€ арифметична швидк≥сть молекул.
- середн€ арифметична швидк≥сть молекул.
—ередню арифметичну швидк≥сть ≥ середню довжину в≥льного проб≥гу молекул знаходимо за формулами
 (3)
(3)
 (4)
(4)
де п - концентрац≥€ молекул, €ку знаходимо ≥з основного р≥вн€нн€ молекул€рно-к≥нетичноњ теор≥њ газ≥в:

де – Ч тиск; k = 1,38×10-23 ƒж/ - стала Ѕольцмана.
“од≥ на основ≥ (4) довжина в≥льного проб≥гу молекули

√устину кисню визначимо за формулою

« урахуванн€м п д≥станемо
 (6)
(6)
ѕ≥дставимо (6), (5), (3) у р≥вн€нн€ (1), тод≥ формула коеф≥ц≥Їнта терт€ набере вигл€ду

ѕ≥дставл€ючи (5), (3) у формулу (2), отримаЇмо розрахункову формулу дл€ коеф≥ц≥Їнта дифуз≥њ

« урахуванн€м (6), к≥нцева формула маЇ вигл€д

ѕ≥дставл€ючи числов≥ значенн€ величин, вз€тих в одиниц€х системи —≤, знаходимо:

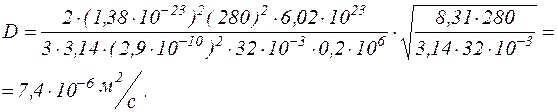 ¬≥дпов≥дь:
¬≥дпов≥дь:  = 2-10-5
= 2-10-5  ; D = 7,4×10-6
; D = 7,4×10-6  .
.
«адача 4.5. ¬изначити середн≥й об'Їм атома у монокристал≥ м≥д≥.
–≥шенн€. «важимо на те. що у випадку, коли в умов≥ задач≥ названо конкретний матер≥ал, то у розв'€зку ми маЇмо право використовувати будь-€к≥ його табличн≥ параметри. «окрема, у даному випадку ми використаЇмо такий табличний параметр, €к густина м≥д≥.
ористуючись пер≥одичною системою елемент≥в, можемо визначити атомну масу м≥д≥: ћ= ј = 64.
«найдемо к≥льк≥сть частинок в одиниц≥ об'Їму

де m- маса м≥д≥ в обТЇм≥ 1 м3
“од≥ об'Їм, що припадаЇ на один атом м≥д≥:

ѕ≥дставивши числов≥ значенн€ величин, вз€тих в одиниц€х системи —≤, знаходимо

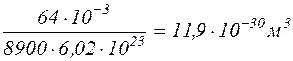
¬≥дпов≥дь:  м3.
м3.






