Системой счисления (счислением, нумерацией) называется совокупность приемов и правил для обозначения и наименования чисел. В любой системе счисления число представляется совокупностью символов, которые называются цифрами. Каждой цифре в записи числа однозначно сопоставляется определенное количество, выражаемое этой цифрой. Это количество называется количественным эквивалентом данной цифры.
Различают непозиционные и позиционные системы счисления. Система счи- сления называется непозиционной, если каждой цифре в любом месте записи числа однозначно соответствует один и тот же количественный эквивалент. Такие системы являются более ранними в историческом плане, например, общеизвестная римская нумерация. Однако непозиционные системы счисления находят ограниченное применение в ВТ, так как они характеризуются очень сложными и громоздкими алгоритмами представления чисел и выполнения арифметических операций.
Система счисления называется позиционной, если одной и той же цифре соответствуют различные количественные эквиваленты в зависимости от номера местоположения (разряда) этой цифры в записи числа. В принципе возможны так- же частично-позиционные системы, в которых для одного множества цифр коли-чественные эквиваленты постоянны, а для другого множества цифр они зависят от их местоположения в записи числа.
Для определения количественного эквивалента полной записи числа исполь-зуется некоторая функция от количественных эквивалентов совокупности цифр в его записи. Если этой функцией является функция сложения, то система счисления называется аддитивной, если умножения – то мультипликативной. Для большинства существующих систем счисления указанная функция является функцией десятич- ного сложения. В этом случае для нахождения количественного эквивалента чис- ла необходимо просуммировать все количественные эквиваленты цифр в его запи- си по правилам десятичной арифметики.
Если в позиционной системе счисления каждая цифра имеет свой опреде-ленный символ, то она называется системой с непосредственным представлением цифр. Наряду с этим существуют системы с кодированным представлением цифр. В таких системах каждая цифра кодируется определенной комбинацией нескольких символов, которые представляют собой цифры другой системы счисления.
Преимущественное распространение в ВТ получили однородные позицион- ные системы счисления. Во всех разрядах числа, представленного в однородной системе, используются цифры из одного и того же множества. Например, в обыч- ной десятичной системе во всех разрядах любого числа используются цифры из множества {0, 1,..., 9}, в двоичной системе — цифры из множества {0, 1} и т. п. В однородной позиционной системе при непосредственном представлении цифр число записывается в виде
(1)
Количественный эквивалент, выражаемый этой записью, определяется так:
(2)
где хi – цифры i -го разряда записи числа, принимающие значения из определенно- го множества, a k называется основанием системы счисления и равно количеству цифр, используемых в данной системе. Величину ki принято называть весом i -го разряда. В n -разрядном слове (1), где п = s + т + 1, целая часть числа представ- лена s + 1 разрядами слева от запятой, а дробная часть – т разрядами справа от запятой. В данном случае вес i -го разряда в k раз больше веса i – 1-го разряда. Такая система счисления называется системой с естественным порядком весов (естественной). Существуют также системы с искусственным порядком весов, для которых указанное соотношение весов соседних разрядов не является обязатель- ным. Известны, например, системы с искусственным порядком весов, в которых целое положительное число X выражается как
где j может принимать одно из значений, принадлежащих множеству {1, 2,..., п }, т.е. j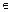 
{ 1, 2,..., п }. При k = 2, j = 3 веса разрядов в такой системе образуют ряд 20, 21, 22, 20 (23 - 1), 21 (23 - 1),... или 1, 2, 4, 7, 14,... Такие системы применяются в средствах ВТ, оптимизированных по некоторым показателям (например, по потребляемой мощности), для создания высоконадежных вычис-лительных средств и для кодирования цифр других систем счисления с большим основанием.
Системы с естественным порядком весов различают также по виду основа- ния k. Известны, например, системы с натуральными, отрицательными, дробными, комплексными основаниями. Наибольшее распространение в ВТ получили системы счисления с натуральными основаниями. Однако другие системы обладают рядом особенностей, которые в некоторых случаях делают их более эффективными, чем системы с натуральными основаниями.
Помимо однородных позиционных систем известны также смешанные (не-однородные) позиционные системы счисления. Смешанные системы также, как и однородные, могут быть с непосредственным и кодированным представлением цифр. Примером смешанной системы с кодированным представлением цифр являя- ется система измерения времени (в годах, месяцах, неделях, сутках, часах и т. д.). Если каждая группа разрядов смешанной системы счисления представлена цифра- ми однородной системы с естественным порядком весов, то смешанная система также является системой с естественным порядком весов.
В общем случае определение системы счисления с естественным порядком весов, которое подходит к смешанным системам и однородным, можно сформу-лировать следующим образом. Система счисления называется системой с естест-венным порядком весов, если в целой части записи числа вес первого (младшего) разряда равен единице, а вес любого другого разряда равен произведению основа- ний, соответствующих каждому из разрядов, расположенных в целой части правее данного разряда; в дробной части записи числа вес любого разряда равен величи- не, обратной произведению оснований, соответствующих данному разряду и разря- дам, расположенным в дробной части слева от него.
Из приведенного определения следует, что веса разрядов смешанных систем счисления определяются по мультипликативному принципу, а количественный эк-вивалент записи числа определяется по аддитивному принципу, т. е. для нахожде- ния количественного эквивалента записи числа необходимо просуммировать веса количественных эквивалентов цифр по правилам десятичной арифметики.
К применяемым вВТ системам счисления предъявляются следующие оче-видные требования.
Однозначность. Каждому числу должно соответствовать единственное его представление в заданной системе и наоборот.
Конечность. Каждому целому числу должно сопоставляться слово конечной длины.
Эффективность. Должен существовать алгоритм, с помощью которого за конечное число шагов осуществлялся бы переход or представления числа конечной длины к самому числу. При переходе от числа к его представлению должны су-ществовать алгоритмы, которые для целого числа реализуют этот переход за ко- нечное число шагов, а для дробного числа — за конечное число шагов позволяют получить представление числа, количественный эквивалент которого отличается от числа не более, чем на заданную величину погрешности.
Системы счисления с натуральным основанием, удовлетворяющие требова-ниям однозначности, конечности и эффективности, называются каноническими. Для таких систем цифра 0 (нуль) является обязательной, а количество различных цифр равно основанию k.
В зависимости от множества цифр, допустимых в каждом разряде, систе- мы счисления делятся на симметричные, смещенные и кососимметричные. Систе- мы счисления с нечетными натуральными основаниями k = 2 r + 1 и цифрами xi 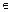{- r,- r + 1,..., 0,..., r }называются симметричными. Такие системы позво- ляют представить любое целое число (как положительное, так и отрицательное) в конечном виде. Если основание системы счисления является четным числом, то построение симметричной канонической системы становится невозможным. При-мером симметричной канонической системы является троичная система (k = 3) с цифрами {-1, 0, 1}.
Если канонические системы с натуральным основанием k имеют только цифры xi 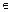{0, 1,..., k - 1} или только цифры xi 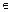{- k + 1, - k + 2,..., 0}, то они называются смещенными. С помощью таких систем можно представить в конечном виде либо только положительное, либо только отрицательное целое число. К указанным системам относятся, например, десятичная система с цифра- ми {0, 1,..., 9} и двоичная система с цифрами {0, 1}.
Кососимметричными каноническими системами называются системы с нату-ральным основанием k и цифрами xi 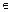{- q,- q + 1,..., 0,..., g }, причем q+g+ 1 = =k, q 
g. Такие системы по своим свойствам занимают промежуточное положение между симметричными и смещенными системами.
При записи чисел в канонических системах счисления в каждом разряде может быть использована одна из k различных цифр. Поскольку общее количест- во различных комбинаций цифр в п разрядах равно kn и числа в таких системах представляются однозначно, то общее количество чисел, которое можно предста- вить с помощью п разрядов, также равно kn.
Подставляя в (2) вместо xi их возможные максимальные и минимальные значения для различных систем, можно определить, что диапазоны представления чисел для симметричных, смещенных с положительными цифрами, смещенных с отрицательными цифрами и кососимметричных систем определяются соответст- венно интервалами
причем любые два ближайшие по значению числа отличаются на единицу младше- го разряда, т. е. на величину k - m.
В ряде случаев для удобства выполнения арифметических операций или повышения надежности представления информации используются позиционные системы счисления с естественным порядком весов, в которых количество различ- ных цифр, допустимых для каждого разряда, превышает основание системы счис-ления.Такие системы счисления удовлетворяют требованиям конечности и эффек- тивности, но не удовлетворяют требованию однозначности и называются избы-точными.
Избыточные системы счисления с натуральным основанием k = 2 r и циф- рами xi 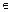{- r, - r +1,..., 0,..., r, r + 1} или основанием k = 2 r + 1 и цифрами xi 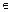{- r - 1, - r,..., 0,..., r, r + 1} называются квазиканоническими.
Примерами таких систем являются десятичная система с цифрами {- 5, - 4, - 3, - 2, - 1, 0, 1, 2, 3, 4, 5, 6} и троичная система с цифрами {- 2, - 1, 0, 1, 2}. Об- щее количество различных цифр в таких системах равно k + 2.
Системы счисления с натуральным основанием k = 2 r и цифрами xi 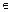{- r, - r + 1,..., 0,..., r - 1, r } или с основанием k = 2 r + 1 и цифрами xi 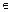{- r, - r + 1,..., 0,..., r, r + 1} называются модифицированными квазиканоническими избыточ- ными системами счисления. В таких системах количество различных цифр лишь на единицу больше основания системы счисления. К модифицированным квазика-ноническим системам счисления относятся, например, троичная система с цифра- ми {- 1, 0, 1, 2} и двоичная система с цифрами {-1, 0, 1). Указанные системы счис- ления могут быть эффективно использованы, например, при выполнении операций умножения и деления.
При выполнении операций деления и извлечения корня находит также применение неканоническая двоичная система счисления с цифрами {-1, 1}. В данной системе вес каждого разряда является целой степенью числа 2, а диапазон представления чисел при естественном порядке весов заключен между максималь- ным числом 11...1,1...11 = 2s+1 - 2-m и минимальным числом 
... , ... = = –2s+1 + 2-m (здесь означает –1). Отсутствие цифры 0 в этой системе приводит к невозможности конечным образом представить любое четное число и нуль.
Большой практический интерес представляют смешанные системы, в кото- рых каждый разряд канонической десятичной системы заменяется несколькими двоичными разрядами с определенными весами.
В системах счисления с естественным и искусственным порядком весов каждый разряд в записи числа имеет свой вес. Такие системы называются также взвешенными или весомозначными. Наряду с этим возможны такие системы счисления, в которых каждая отдельная цифра никак не связана с каким-либо количественным эквивалентом и лишь определенным комбинациям цифр ставится в соответствие некоторый количественный эквивалент. Такие системы счисления на-зываются невзвешенными (невесомозначными, символическими).
Главное преимущество взвешенных систем счисления состоит в удобстве представления чисел и простоте выполнения арифметических операций. Недоста- ток таких систем заключается в невозможности выполнения арифметических опе- раций как поразрядных. Поразрядной операцией называется такая операция, ре- зультат которой в любом разряде не зависит от результата выполнения этой опе- рации во всех остальных разрядах. Примером системы счисления, в которой ариф-метические операции могут выполняться поразрядно, является система остаточных классов (СОК), являющаяся невзвешенной системой. В СОК для представления це- лых положительных чисел выбирается набор взаимно простых модулей (оснований) Рi (i = 
) таким образом, чтобы выполнялось условие X max < P1P2...Pm,где Х mах – максимальное из представляемых чисел. Любое целое положительное число X представляется в виде
X = (X 1, X 2, …, X m),
|
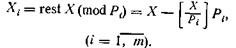
где Хi — целочисленный остаток (вычет) от деления X на модуль Pi,т. е.
Запись [ А ]означает округление А в сторону ближайшего меньшего целого числа, если А дробное ([ А ] = int А). Максимальное количество чисел, которое можно представить с помощью т модулей, равно N = Р1Р2...Рт . В табл.1 приве- дено изображение некоторых чисел при использовании системы модулей Р1 = 2,Р2 = 3 и Р3 = 5.
Таблица 1.
| Десятичное число | Запись числа в СОК(Р1 = 2; Р2 = 3; Р3 = 5) | Десятичное число | Запись числа в СОК(Р1 = 2; Р2 = 3; Р3 = 5) |
| 0 0 0 | 1 2 1 | ||
| 1 1 1 | 0 0 2 | ||
| 0 2 2 | 1 1 3 | ||
| 1 0 3 | 0 2 4 | ||
| 0 1 4 | 1 0 0 | ||
| 1 2 0 | 0 1 1 | ||
| 0 0 1 | 1 2 2 | ||
| 1 1 2 | 0 0 3 | ||
| 0 2 3 | 1 1 4 | ||
| 1 0 4 | 0 2 0 | ||
| 0 1 0 |
К недостаткам СОК, затрудняющим ее применение в ВТ, относятся: отсут-ствие удобного способа сравнения чисел; трудность выполнения операции деления и округления; отсутствие удобного способа определения выхода результата опера- ции за пределы диапазона допустимых чисел. Указанные недостатки ограничивают область применения СОК рамками специализированных ЭВМ, для которых эти недостатки не являются существенными.
Выбор системы счисления для представления информации в ЭВМ оказыва- ет существенное влияние на ее надежность и экономичность. От используемой системы счисления зависит структура аппаратных средств машины, удобство и ско-рость выполнения арифметических и логических операций. Необходимо учитывать также простоту перевода чисел в десятичную систему счисления, так как общение человека с машиной строится на основе десятичной системы независимо от сис- темы, используемой для представления информации в самой машине. Практика разработки и эксплуатации ЭВМ показывает, что вычислительные машины, предназначенные для решения задач, в которых количество вычислительных операций, приходящихся на один символ вводимой-выводимой информации, велико, как пра-вило, проектируются с использованием двоичной системы счисления. К таким за- дачам относится широкий круг научно-технических задач, задачи оптимального планирования, транспортные задачи и др. В ЭВМ, где время ввода – вывода дан- ных значительно превышает время обработки информации, а также в малых уни-версальных ЭВМ, характеризующихся интенсивным обменом информацией между человеком и машиной, применяется десятичная система счисления.
В последние годы, особенно в связи с разработкой АСУ, в функции кото- рых входит решение широкого круга разнообразных задач, проявляется тенденция к созданию вычислительных комплексов, имеющих в своем составе как двоичные, так и десятичные устройства обработки информации.
