÷ель работы: »зучить принцип суперпозиции магнитных полей на примере определени€ горизонтальной составл€ющей магнитного пол€ «емли.
ѕриборы и принадлежности: »сточник посто€нного тока (G4), тангенс-гальванометр (тг), амперметр(ј), переключатель (S2), реостат (R14).
“еоретическое введение:
«емл€ представл€ет собой огромный магнит, который в окружающем «емлю пространстве создает магнитное поле. ћагнитные полюсы «емли не совпадают с географическими полюсами и со временем измен€ют свое положение. ¬ектор индукции магнитного пол€ «емли на экваторе направлен горизонтально, у магнитных полюсов «емли - вертикально и всюду в других местах- под некоторым углом к горизонтальной плоскости. Ќаправление вектора магнитной индукции пол€ «емли можно определить с помощью магнитной стрелки NS, подвешенной на тонкой нити (рис. 1). ћагнитна€ стрелка устанавливаетс€ по направлению вектора B. ¬ертикальна€ плоскость, в которой установитс€ стрелка, называетс€ плоскостью магнитного меридиана. “ак как магнитные полюса не совпадают с географическими, то стрелка будет отклонена от географического меридиана на некоторый угол a, который называют магнитным склонением. Ќа рис 1 угол магнитного склонени€ представлен как угол между плоскост€ми магнитного и географического меридианов. ”гол, который образует магнитна€ стрелка с горизонтальной линией, лежащей в плоскости магнитного меридиана называют магнитным наклонением Q.










 a ¬ Bв ¬
a ¬ Bв ¬

 ј Q
ј Q
Bг
–ис.1 –ис. 2
A- плоскость географического меридиана. ƒл€ случа€, когда плоскость B- плоскость магнитного меридиана совпадает с плоскостью ZOY.
¬ектор индукции  магнитного пол€ «емли можно разложить на две составл€ющие: горизонтальную
магнитного пол€ «емли можно разложить на две составл€ющие: горизонтальную  г и вертикальную
г и вертикальную  в (рис. 2) ¬еличины
в (рис. 2) ¬еличины  г, a, Q - называют элементами земного магнетизма.
г, a, Q - называют элементами земного магнетизма.
≈сли магнитна€ стрелка может вращатьс€ только вокруг вертикальной оси, то она будет устанавливатьс€ лишь под действием  г. Ёто свойство используетс€ дл€ определени€ величины
г. Ёто свойство используетс€ дл€ определени€ величины  г с помощью специального прибора называемого тангенс-гальванометром.
г с помощью специального прибора называемого тангенс-гальванометром.
“ангенс-гальванометр представл€ет собой плоский вертикальный виток радиуса R, в центре которого в горизонтальной плоскости расположена магнитна€ стрелка, способна€ вращатьс€ только вокруг вертикальной оси (–ис.3а) ¬ыберем пр€моугольную систему координат таким образом, чтобы плоскость витка совпадала с плоскостью ZOY, лежащей в плоскости магнитного меридиана, а магнитна€ стрелка NS вращалась вокруг вертикальной оси, помещенной в точке O, при этом плоскость вращени€ магнитной стрелки совпадает с плоскостью XYZ. ѕри отсутствии тока в витке стрелка устанавливаетс€ в плоскости магнитного меридиана ZOY. ѕри пропускании тока по витку в центре его возникает магнитное поле, величину индукции которого можно определить, использу€ закон Ѕио-—авара- Ћапласа в общем виде:
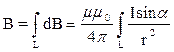 dL (1)
dL (1)
 где L - длина проводника произвольной формы, r - рассто€ние от точки пространства где определ€етс€ поле dB до элемента проводника dL создающего это поле, I - ток проводника, a - угол между направлени€ми тока I и радиуса вектора r, m - относительна€ магнитна€ проницаемость среды(дл€ воздуха m =1), m0 - магнитна€ посто€нна€ равна€ 4p10-7 √н/м.
где L - длина проводника произвольной формы, r - рассто€ние от точки пространства где определ€етс€ поле dB до элемента проводника dL создающего это поле, I - ток проводника, a - угол между направлени€ми тока I и радиуса вектора r, m - относительна€ магнитна€ проницаемость среды(дл€ воздуха m =1), m0 - магнитна€ посто€нна€ равна€ 4p10-7 √н/м.
|
|
|
 |
Z
–ис.3 а –ис.3 б
ƒл€ случа€ кругового тока a = 900, r = R (где R - радиус витка) имеют посто€нные значени€ дл€ всех участков dL (рис.3 б). ƒлина проводника в этом случае L = 2pR. ѕоэтому, в соответствии с формулой (1) индукци€ магнитного пол€ B в центре кругового тока равна:
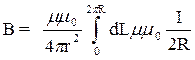 (2)
(2)
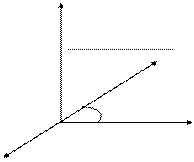
ѕод действием индукции  магнитна€ стрелка повернетс€ на некоторый угол j, устанавлива€сь в направлении равнодействующей индукции двух полей
магнитна€ стрелка повернетс€ на некоторый угол j, устанавлива€сь в направлении равнодействующей индукции двух полей  и
и  рис. 4. »з рисунка 4 видно,
рис. 4. »з рисунка 4 видно,
что 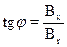 или
или 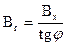
подставл€€ в это уравнение значение ¬х из уравнени€ (2) получим:
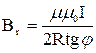 (3)
(3)
«на€ величины тока I и угла j можно
определить значение Br. ≈сли вместо одного
витка с током I вз€ть короткую катушку, ¬х
 состо€щую из n витков, то величина Br ¬х
состо€щую из n витков, то величина Br ¬х
 будет в n раз больше S
будет в n раз больше S
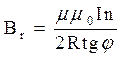 (4) j
(4) j
¬г
N
R=100 мм - радиус, n = 10 - число витков.
–ис. 4






