Элементы дифференциального исчисления функции двух переменных

 

Если каждой паре двух независимых переменных (x, y) соответствует единственное значение z, то z = z(x, y) называется функцией двух переменных.

Пример: найти D(z), если .

 

Графиком функции двух переменных является поверхность.

Пример: ,

– частное приращение по x.

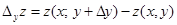– частное приращение по y.

– полное приращение функции z.

Пример: найти

· Частной производной функции z по переменной x называется .

· Частной производной функции z по переменной y называется .

Пример: найти .

.

ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВТОРОГО ПОРЯДКА.

Утверждение: Если смешанные частные производные непрерывны в точке, то они равны в этой точке.

Пример: , найти частные производные второго порядка.

ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ.

Частные дифференциалы по x и y получаются, если фиксировать одну из переменных.

Полное приращение функции:

1) – фиксирована.

По теореме Лагранжа:

(1) .

2) x – фиксирован, аналогично получаем:

(2)

Первые два слагаемых главная часть приращения.

Последние два – бесконечно малые более высокого порядка, чем первые два.

Главная часть полного приращения функции двух аргументов называется полным дифференциалом.

Пример: Найти .

Понятие полного дифференциала полностью аналогично дифференциалу одной переменной.