Энергия магнитного поля. Закон электромагнитной индукции устанавливает связь между электрическим и магнитным полем. Электрическое поле между обкладками конденсатора сосредотачивает в себе определенную энергию. Аналогичным образом магнитное поле, окружающее катушку индуктивности, имеет свою суммарную энергию, которую также можно вычислить.
Работа электрического тока, изменяющегося во времени, приводит к возникновению магнитного поля W вокруг катушки индуктивности, в которой течет ток:
LI 2
A = W =, (3.6.1)
где индуктивность L определяется соотношением Ф = LI, т.е. представляет собой коэффициент пропорциональности меду током и магнитным потоком.
Колебательный контур представляет собой цепь из элементов, соединенных последовательно: катушки с индуктивностью L и конденсатора с емкостью C (рис. 3.18).
Рис. 3.18. Элементарный колебательный контур
Если разомкнуть контур и тем самым зарядить конденсатор, то между его обкладками появится электрическое поле. Если далее замкнуть конденсатор на катушку индуктивности, то конденсатор начнет разряжаться. При этом в контуре возникнет электрический ток разряда конденсатора, а в ка-
тушке индуктивности появится магнитное поле. Электрическое поле в конденсаторе исчезнет совсем, а вся его энергия перейдет в энергию магнитного поля. Далее изменяющееся магнитное поле вызовет индукционный ток, который в соответствии с правилом Ленца будет стремиться поддержать ток разряда конденсатора. Конденсатор будет перезаряжаться и между его обкладками возникнет электрическое поле. Магнитное поле исчезнет совсем, его энергия превратится в энергию электрического поля. Уравнение свободных колебаний в колебательном контуре выглядит следующим образом:
d Q +
1 Q = 0, (3.6.2)
dt 2 LC
здесь Q (t) – зависимость заряда на обкладках конденсатора от времени.
Это уравнение аналогично уравнению свободных гармонических колебаний пружинного маятника (1.5.4). В стационарном состоянии заряд создает электрическое поле на обкладках конденсатора. Затем, перетекая с одной пластины, на другую, он преобразует электрическое поле в магнитное. Это происходит с некоторой частотой, характерной для заданного LC -контура.
В результате этого происходит периодическое превращение энергии электрического поля между обкладками конденсатора в энергию магнитного поля катушки индуктивности и обратно. Суммарная энергия электрического и магнитного полей для LC -контура при отсутствии активного сопротивления цепи остается неизменной:
LI 2
CU 2
W = + = const. (3.6.3)
2 2
Уравнения Максвелла. Развивая идеи Фарадея, шотландский ученый Джеймс Максвелл создал классическое представление об электромагнитном поле, содержащем в общем случае и электрическое и магнитное поля, связанные между собой и способные взаимно превращаться друг в друга. Он также составил систему из четырех уравнений, с помощью которых можно описать эти превращения. В отсутствие диэлектриков и магнетиков они имеют следующий вид в интегральной форме:
Ø EdS= Q, (3.6.4)
ɛ 0
Ø BdS= 0, (3.6.5)
Ø Edl= d0B, (3.6.6)
dt
Ø Bdl= µ0I+ µ0 ɛ 0
d0E
dt
. (3.6.7)
Уравнение (3.6.4) связывает электрическое поле с его источниками, электрическими зарядами: поток электрического поля через замкнутую поверхность равен полному заряду, заключенному внутри нее.
Уравнение (3.6.5) выражает отсутствие магнитных зарядов и объясняет замкнутость силовых линий магнитного поля.
Уравнение (3.6.6) – это закон электромагнитной индукции Фарадея, показывающий наличие связи между магнитным и электрическим полем. Он утверждает, что изменение потока магнитной индукции позволяет получить переменное электрическое поле.
Уравнение (3.6.7) было написано самим Максвеллом. Он, анализируя закон Ампера, пришел к выводу, что магнитное поле создается не только электрическим током, но и переменным электрическим полем. Последнее слагаемое (3.6.7) по смыслу означает, что изменение потока электрического поля Ф E (по аналогии с током проводимости Максвелл назвал эту составляющую током смещения I см) через некоторую поверхность приводит к возникновению переменного магнитного поля:
Ø Bdl= µ0I+ µ0 ɛ 0
d0E
dt
= µ0(I + Iсм). (3.6.8)
Последние два уравнения (3.6.6) и (3.6.7) демонстрируют взаимосвязь электрического и магнитного полей. Они показывают, что переменное магнитное поле порождает электрическое поле, а переменное электрическое поле создает магнитное поле.
Таким образом, уравнения Максвелла содержат в себе все основные законы электрического и магнитного полей и поэтому являются общими уравнениями электромагнитного поля в покоящихся средах.
Электромагнитные волны. Электрический заряд, кото-
рый совершает колебания, двигается ускоренно и
поэтому
излучает энергию. По теории Максвелла он является источником электромагнитных волн. Тогда колебания электрического поля в точке x описываются выражением (аналогично
механическим колебаниям, являющимся нических волн по формуле (1.6.3)):
источником меха-
, (3.6.10)
где
– время распростране-
ния колебаний от начальной точки до точки x, E 0– амплитуда колебаний электрического поля, v – скорость распространения волны. Аналогично колебания напряженности магнит-
ного поля
в точке с координатой x:
,
(3.6.11)
где E 0– амплитуда колебаний электрического поля, v – скорость распространения волны.
Эти формулы выражают законы изменения электриче-
ского и магнитного
полей, они называются уравнениями
плоской гармонической электромагнитной волны.
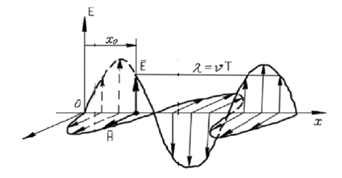
На рис. 3.19 представлен график плоской электромагнит-
ной волны. Векторы
E, H, v перпендикулярны друг другу.
Электромагнитные волны в отличие от механических волн, могут распространяться не только в различных средах, но и в вакууме.
Рис. 3.19. График плоской электромагнитной волны
Длина электромагнитной волны ß = rT = r. Из теории
v
Максвелла следует, что скорость распространения электро-
магнитных волн в вакууме (скорость света с) составляет
1 м
rвак== 3 · 108 = c. (3.6.12)
ƒs0µ0 с
В веществе скорость распространения электромагнитных волн уменьшается в √sµ раз:
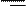r = c
√sµ
= 1
ƒs0µ0sµ
, (3.6.13)
где диэлектрическая ε и магнитная μ проницаемости среды зависят от электрических и магнитных свойств сред. Из приведенных выше соотношений можно сделать вывод, что свет
– это электромагнитная волна.
Распространяясь в пространстве, электромагнитные волны несут энергию. Из выражений для плотностей энергии электрического и магнитного полей
U = 1 e e E 2,
E 2 0
1 B 2
U B =
2 m 0 m
(3.6.14)
можно получить выражение для плотности энергии электромагнитных волн:
. (3.6.15)
2 2 m 0 m
Энергия, переносимая волной в единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны, называется плотностью потока энергии электромагнитного излучения или вектором Пойнтинга 29. Его направление совпадает с направлением
распространения электромагнитной волны, т.е. электромагнитная волна несет энергию в направлении своего распространения.
29 Плотность потока энергии величина скалярная, поскольку представляет собой отношение энергии к объему, в котором она находится. Вектор Пойтинга означает, что энергия распространяется в том же направлении, что и волна.
