Методы определения показателей структурной надежности

 

Аналитические методы

Рассмотрим задачу определения вероятности связности меж­ду узлами а_S и а_t, если задано множество путей M_St, которые могут быть использованы для этой связи, и извест­ны надежность 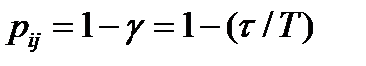всех ребер сети, образующих пути. Надежность пути , при условии статистической независимости элементов сети, оценим вероятностью одновременного работоспособного состояния всех ребер, образующих этот путь, т. е.

(5.3)

где – показатель надежности линии ij, принадлежащей пути между узлами s и t.
Если учитывать надежность узлов, то

(5.4)

где – показатель надежности i – ого узла, входящего путь между узлами s и t.

Вероятность связности двух узлов а_s и a_t будем оценивать вероятностью исправного состояния хотя бы одного пути из заданного множества . Когда отдельные элементы пути (их участки или линии связи) составляют параллельно-последовательную структуру, то для определения вероятности связности можно использовать обычные методы определения надежности структур с таким соединением элементов. При последовательном соединении можно пользоваться формулой (11.1), а при параллельном соединении элементов общая надежность рассчитывается по формуле

, (5.5)

где pi- надежность каждого элемента;

n- число параллельно соединенных элементов.

На рисунке 5.2 приведен пример параллельно-последовательной структуры

и с мостиковым соединением по отношению к узлам 1и 6.

Рис. 5. 2 Пример структур сети параллельно-последовательной (а) и с мостиковым соединением (б_) по отношению к узлам 1 и 6

Если в структуре сети имеются мостиковые соединения, то ис­пользовать приведенный выше метод расчета нельзя. Напри­мер, для структуры рис. 2б, отличающейся от структуры рис.2а наличием ребра b₂₅. Одним из методов расчета вероятности связности (надежности свя­зи) Pst между узлами as и at для сложной структуры является метод последовательного разложения структуры. 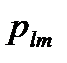Метод основан на том свойстве, что надежность структуры (рис 11.3), включаю­щей ребро с надежностью , рав­нa:

, (5.6)
г де - надежность связи в сети, в которой p_lm=1, т. е. узлы а_l и а_m слиты;
- надежность связи в сети при p_Lm = 0, т. е. из сети изъято ребро b_lm.

Разложение (вынос ребер) производится до тех пор, пока ос­тавшиеся структуры не будут параллельно-последовательными. Метод последователь-ного разложения позволяет определить потенциальную надежность связи между заданными узлами в виде функции или числового значения. Однако он не работает в случае, если необходимо определить надежность заданного мно­жества путей m_st, меньшего, чем множество всех путей между узлом s и t.
Для определения вероятности связности узла s с узлом t в этом случае можно воспользоваться следующей методикой:

1. Определим список путей, которые могут быть использованы для связи узла s с узлом t.

2. Каждому пути поставим случайное событие Ak, характеризующее исправное состояние данного пути.

3. Определим надежность каждого из указанных путей c учетом заданных

показателей надежности элементов сети. Полученная функция определяет

вероятность наступления события Ak.

4. Воспользуемся формулой для расчета вероятности суммы совместных событий Ai,поставленных в соответствие множеству путей между узлами

s и t.

(5.7)

где t - число путей, которые могут быть использованы для связи узла i с узлом j;

Ai– событие, поставленное в соответствие i-ому исправному пути из множества путей k=(1,t);

P(А_i) – вероятность наступления события А_i;

P(А_i А_j) – вероятность совместного наступления двух событий А_к и А_m;

P(А₁ А₂ …А_t) – вероятность совместного наступления t событий Аi;

P (UA_i) – вероятность наступления хотя бы одного события А_i из мно-жества k=(1,t).

С учетом условия совместного наступления событий Аi, показатели коэффициентов готовности элементов сети, входящих в любое из указанных выше выражений в формуле для расчета вероятности суммы совместных событий, заменяются на первую степень.
Для определения математического ожидания числа связей в сети М (Х) воспользуемся следующим алгоритмом:

· Определим число интересующих нас пар взаимодействующих узлов сети.

· Определим списки путей, которые могут быть использованы для доставки информации для каждой пары узлов сети из заданного списка.

· Для каждой пары узлов определим вероятность их связности по

выше изложенной методике.

· Произведем суммирование значений вероятностей связности различных пар узлов сети.

В результате получим абсолютное значение математического ожидания числа связей сети – М (Х). Удобнее и нагляднее данную величину выразить в относительных единицах. Тогда величина М (Х)_отн. может быть рассчитана по формуле:

М (Х)_отн. = (М (Х)/N_max)·100%, (5.8)

где N_max – максимальное (заданное) число связей в сети при условии, что все элементы сети абсолютно надежны.

Метод статистических испытаний

Наиболее универсальным методом, который пригоден для решения задач практически любой сложности, является метод статистических испытаний (метод Монте-Карло). Метод заключается в построении математической модели системы, реализация которой осуществляется в виде программы для ЭВМ.

Основная идея этого методаосновывается на наличии связи между вероятностными ха­рактеристиками различных случайных процессов и величинами, явля­ющимися решениями задач математического анализа. Вместо вычисления ряда сложных аналитических выражений можно эк­спериментально определить значения соответствующих вероятностей или математических ожиданий. Этот метод получил широкое развитие в связи с новыми возможностями, которые дают современные ЭВМ.

В основе метода лежит техника генерации конечных наборов значений случайной величины в соответствии с ее функцией распре­деления вероятностей. Будем предполагать, что в рамках метода статических испытаний существует возможность воспроизвести слу­чайную последовательность значений случайной величины или слу­чайную последовательность значений объекта, если задана функция распределения этой величины или распределение вероятностей сос­тояний объекта. Метод статических испытаний обычно используется для опреде­ления с ограниченной точностью того или иного стохастического параметра объекта “a “ путем вычисления его несмешанной выборочной оценки a^*_N на основании имитации механиз­ма возникновения случайной величины или случайного события. Не­который стохастический параметр “a” распределения случайной величины Х обладает несмешtнной выборочной стохастической оценкой a^*_N , вычисляемой по случайной выборке ограниченного объема N, если(a - a^*_N ) 0 при N. Точность вычисляемой оценки растет с увеличением объема выборки N.
Однако увеличение объема выборки сопровождается обычно линейным возрастанием трудоемкости, так что неизбежно возникает необходи­мость ограничить объем выборки минимальным числом испытаний, достаточным для получения требуемой точности.
Наиболее универсальным и простым способом регулирования объема выборки по точности является автостоп, который организует­ся следующим образом. В ходе эксперимента по мере накопления числа испытаний анализируется последовательность выборок объема 1,2… К. Для очередной К - той выборки вычисляется значение выборочной оценки a^*_N и сравнивается с вычисленным ранее a^*_{N к-1} ; a^*_{N к-2} ; a^*_{N к-v}. Эксперимент прекращается в случае равенства всех сравниваемых величин с требуемой точно­стью, а в качестве искомой оценки берется любая из них.

Число v -предшествующих значений оценки сравниваемых с очередным значением, определяет степень гарантии достижения требуемой точ­ности. Использование автостопа базируется на допущении, что величины (a - a^*_{N к} ) и (a^*_{N к} - a^*_{N к-1}) убывают монотонно с ростом числа испытаний. Основное неудобство автостопа -объем выборки, необходимой для получения требуемой точности выборочной оценки, нельзя опре­делить заранее. Даже оценить этот объем можно только в отдельных случаях, когда зависимость точности оценок a^*_N от N удается выразить аналитически.

Увеличение точности, например, в десять раз приводит к сто­кратному удлинению времени решения задачи (числа испытаний). По­этому метод статических испытаний не может быть использован для получения решений с очень большой точностью. В практических задачах этот метод дает точность порядка 0,01-0,001 от максимального значения. Метод статических испытаний хорошо приспособлен к многомер­ным задачам. Обычно эти задачи и не требуют большой точности, поэтому отмеченный недостаток метода не столь существенен.

Особенности этого метода сводятся к следующему:

· сравнительная простота и однородность последовательности