При измерениях с многократными наблюдениями обработка результатов проводится по-разному в зависимости от числа серий наблюдений, а также от условий и числа наблюдений в каждой серии, значимости систематических погрешностей, законов распределения случайных погрешностей и ряда других факторов. В простейшем случае примем одну серию наблюдений с n = 24 и когда невозможно оценить и исключить систематические погрешности.
1. Снять n = 24 независимых результатов наблюдений и занести в таблицу.
2. Определить математическое ожидание (среднее арифметическое):
3. Определить среднее квадратичное отклонение (СКО) или рассеивание единичных результатов по приближенной формуле Бесселя
D = s 2,
где D – дисперсия.
Качество и точность измерений тем выше, чем меньше СКО, тем меньше вероятность рассеивания результатов наблюдений D.
4. Если x i – mx > ±3s, то необходимо убрать грубые отсчеты (промахи) и снова повторить п. 2, п. 3.
5. СКО среднего арифметического 
6. Проверить гипотезу, что результаты наблюдений принадлежат нормальному закону распределения вероятности.
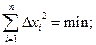
где D xi = xi – mx.
7. Построить кривые рассеивания результатов измерений и погрешностей согласно нормальному закону распределения вероятности, которые показаны на рис. 1.15.
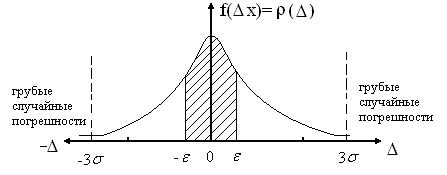
Рис. 1.15. Кривые нормального распределения
8. Определить доверительные границы e случайной погрешности при заданной доверительной вероятности P = 0,95. P = 0,95 принято в технических измерениях для единообразия оценки случайных погрешностей.
,
где 
= 2,064– коэффициент Стьюдента при n = 24.
9. Определить границы суммарной неисключенной систематической погрешности (НСП) результата измерений при условии равномерного распределения НСП.
,
где Qi – граница НСП; k=1,1 – коэффициент, определяемый принятой в технических расчетах доверительной вероятностью P = 0,95; m – количество НСП.
Если m = 0, то e = q.
10. Определить доверительные границы погрешности результата измерений D.
Если 
или 
, то НСП пренебрегаем и граница погрешности результата: DГ = ±e.
Если 
или 
, то случайной погрешностью можно пренебречь и граница погрешности результата: DГ = ±q.
Если оба неравенства не выполняются, то вычисляют СКО среднего арифметического групп наблюдений:
При отсутствии НСП и для одной группы наблюдений: Så = s.
Тогда границы погрешности результата измерений DГ равны 
,
где 
или 
.
11. Записать окончательный результат измерений в сокращенной форме:
X ± DГ, P.
Или в более полной форме:
mx, 
, n, q, P.
Качество и точность измерений тем выше, чем меньше СКО, тем меньше вероятность рассеивания результатов наблюдений D, тем больше вероятность P того, что большинство случайных погрешностей в них мало.
ДЕ3. Правовые основы обеспечения единства измерений. Структура и за
дачи государственной метрологической службы. Основные положения государ-
ственной системы стандартизации и сертификации; международная организа
ция по стандартизации (ИСО). (4ч)
