4.1 ѕохибки вим≥рювань
ѕохибка вим≥рювань Ц це в≥дхиленн€ результат≥в вим≥рюванн€ в≥д д≥йсного значенн€ вим≥рювальноњ величини. ѕохибки представл€ють собою суму ц≥лого р€ду складових, кожна з €ких маЇ свою причину.
ќсновн≥ причини виникненн€ похибок повТ€зан≥ з:
- не€к≥сною наладкою «¬“ або зм≥щенн€м р≥вн€ наладки п≥д час експлуатац≥њ «¬“;
- неправильною експлуатац≥Їю «¬“ (не п≥дтримують умови експлуатац≥њ);
- д≥Їю зовн≥шн≥х фактор≥в на «¬“ та обТЇкт вим≥рюванн€ (температура, магн≥тне поле, в≥брац≥њ, тиск та ≥нш.);
- властивост€ми обТЇкта вим≥рювань;
- квал≥ф≥кац≥ю оператора;
- ≥ншими причинами.
јнал≥зуючи причини, в першу чергу необх≥дно ви€вити т≥, що мають найб≥льший вплив.
4.2 расиф≥кац≥€ похибок вим≥рювань
а) ” залежност≥ в≥д форми вираженн€ похибки вим≥рювань под≥л€ютьс€ на абсолютну ≥ в≥дносну.
јбсолютна (D) Ц це похибка вим≥рюванн€, що виражаЇтьс€ в тих одиниц€х, що ≥ вим≥рювальна величина ≥ €вл€Ї собою р≥зницю м≥ж результатом вим≥рюванн€ ј та ≥стинним ’≥ст (д≥йсним ’д) значенн€м вим≥рювальноњ величини.
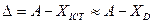
¬≥дносна (d) Ц €вл€Ї собою в≥дношенн€ абсолютноњ похибки вим≥рюванн€ до д≥йсного значенн€ вим≥рюваноњ величини, виражена в процентах або дол€х вим≥рюваноњ величини.

якщо в дол€х, то:

б) ¬ залежност≥ в≥д умов та режим≥в вим≥рюванн€ в≥др≥зн€ють статичну ≥ динам≥чну похибку.
—татична Ц це похибка, що не залежить в≥д швидкост≥ зм≥ни вим≥рюваноњ величини в час≥.
ƒинам≥чна Ц це похибка, що залежить в≥д швидкост≥ зм≥ни вим≥рюваноњ величини в час≥. ƒинам≥чна похибка звТ€зана з ≥нерц≥йн≥стю вим≥рювальних ланок «¬“, тобто з тим, що перетворенн€ у вим≥рювальних ланках не проходить миттЇво.
в) ¬ залежност≥ в≥д характеру про€вленн€, можливостей л≥кв≥дац≥њ ≥ причин виникненн€, похибки под≥л€ютьс€ на систематичн≥ ≥ випадков≥.
—истематична Ц це похибка, що залишаЇтьс€ пост≥йною або законом≥рно зм≥ною при повторних вим≥рюванн€х одн≥Їњ ≥ т≥Їњ ж величини.
ѕричини виникненн€ систематичних похибок:
- зношенн€ робочих поверхонь «¬“, з допомогою €ких зд≥йснюЇтьс€ контакт з вим≥рювальним механ≥змом;
- зм≥ни пружних властивостей деталей, а також њх природнЇ стар≥нн€;
- похибки градуюванн€ (нанесенн€ в≥дм≥ток шкали);
- зб≥льшенн€ щ≥лин у вим≥рювальному механ≥зм≥;
- в≥дхиленн€ реальних елемент≥в схеми в≥д розрахункових ≥ т.д.
- ÷≥ похибки можуть зовн≥шньо себе не про€вити ≥ њх можна знайти при пов≥рц≥ ≥ кал≥бруванню, коли «¬“ пор≥внюють з еталонами.
¬ипадкова Ц це похибка, €ка зм≥нюЇтьс€ випадковим шл€хом при повторних вим≥рюванн€х одн≥Їњ ≥ т≥Їњ ж величини.
Ќезалежно в≥д того, €к би ми сумл≥нно не проводили вим≥рюванн€ в одних ≥ тих же умовах одн≥Їњ ≥ т≥Їњ ж величини, результат може в≥др≥зн€тись один в≥д одного. ¬ипадкова похибка виникаЇ при одночасн≥й д≥њ багатьох джерел, кожне з €ких може мати непом≥тний вплив, але сумарна д≥€ вс≥х джерел може бути досить впливовою.
ѕри вим≥рюванн€х вид≥л€ють також груб≥ похибки або промахи, що про€вл€ютьс€, €к правило, через помилки оператор≥в або р≥зноњ зм≥ни умов проведенн€ вим≥рювань (в≥брац≥€, прот€ги та ≥нш.).
|
|
|
якщо промахи знаход€ть, то при обробц≥ результат≥в вим≥рювань њх не враховують.
4.3 «акони розпод≥лу випадкових похибок
–озгл€немо такий приклад: припустимо, що Ї предмет, довжина €кого вим≥р€на за допомогою робочого еталона Ц оптичного м≥кроскопа ≥ вона дор≥внюЇ 93.147 мм. “епер цей предмет вим≥р€Їмо за допомогою л≥н≥йки, штангенциркул€ ≥ м≥крометра.
÷≥на под≥лки: л≥н≥йки - 1 мм
штангенциркул€ - 0.1 мм
м≥крометра - 0.01 мм
ќтримаЇмо результати вим≥рювань:
- з допомогою л≥н≥йки: lл=93-94 мм
- з допомогою штангенциркул€ lшт=93.1-93.2 мм
- з допомогою м≥крометра lмк=93.14-93.15 мм
јбсолютна похибка складаЇ:
Dл=93-93.147=-0.147 мм
Dшт=93.1-93.147=-0.047 мм
Dмк=93.14-93.147=-0.007 мм
≤з наведеного видно, що абсолютна похибка залежить €к ≥ в≥д похибки конкретного «¬“, так ≥ в≥д похибки робочого еталону, за допомогою €кого визначено Уд≥йснеФ значенн€ вим≥рювальноњ величини.
ѕри в≥дсутност≥ робочого еталону можна визначити похибку результату вим≥рюванн€ на основ≥ результат≥в, отриманих за допомогою конкретних «¬“ (л≥н≥йка, штангенциркуль, м≥крометр). « ц≥Їю метою ≥ введено пон€тт€
густини розпод≥лу ймов≥рностей ≥ функц≥њ розпод≥лу ймов≥рностей.
Ќехай Ї т≥льки два прилади дл€ вим≥рюванн€ довжини того ж предмета Ц цифровий м≥крометр ≥ аналоговий м≥крометр, ц≥на под≥лки €ких 0.01 мм. ¬им≥р€Їмо 100 раз одним ≥ другим приладом даний предмет. –езультати цих вим≥рювань занесемо в таку таблицю:
“аблиц€ 4.1 Ц –езультати вим≥рювань
| ≥льк≥сть однакових результат≥в | ’≥ цифрового «¬“ | Yi аналогового «¬“ | –(’≥) | F(Xi) |
| 93.11 | 93.10-93.11 | 0.02 | 0.02 | |
| 93.12 | 93.11-93.12 | 0.05 | 0.07 | |
| 93.13 | 93.12-93.13 | 0.10 | 0.17 | |
| 93.14 | 93.13-93.14 | 0.20 | 0.37 | |
| 93.15 | 93.14-93.15 | 0.24 | 0.61 | |
| 93.16 | 93.15-93.16 | 0.19 | 0.80 | |
| 93.17 | 93.16-93.17 | 0.11 | 0.91 | |
| 93.18 | 93.17-93.18 | 0.05 | 0.96 | |
| 93.19 | 93.18-93.19 | 0.03 | 0.99 | |
| 93.2 | 93.19-93.2 | 0.01 | 1.00 | |
| Z=100=n |
ƒе:

Ќа основ≥ отриманих результат≥в побудуЇмо так≥ граф≥ки: –(’≥) ≥ F(Xi) в залежност≥ в≥д найменшого ≥ найб≥льшого вим≥р€ного значенн€.
–(’≥)
0.30
| 0.25 | ||||||||||
 0.20 0.20
| ||||||||||
| 0.15 | ||||||||||
| 0.10 | ||||||||||
| 0.05 | ||||||||||
| 0.00 | ||||||||||
| 93.11 | 93.12 | 93.13 | 93.14 | 93.15 | 93.16 | 93.17 | 93.18 | 93.19 | 93.2 |
’≥
–исунок 4.1 Ц √раф≥к розпод≥лу ймов≥рностей
1 Ц густина розпод≥лу ймов≥рностей;
2 Ц пол≥гон розпод≥лу ймов≥рностей.
F(Xi) 1.2
| 0.8 | ||||||||||
 0.6 0.6
| ||||||||||
| 0.4 | ||||||||||
| 0.2 | ||||||||||
| 0.00 | ||||||||||
| 93.11 | 93.12 | 93.13 | 93.14 | 93.15 | 93.16 | 93.17 | 93.18 | 93.19 | 93.2 |
’≥
|
|
|
–исунок 4.2 Ц √раф≥к функц≥њ розпод≥лу ймов≥рностей.
√раф≥к залежност≥ –(’≥) називають густина розпод≥лу ймов≥рностей, ф≥зичний зм≥ст €коњ Ї: величина –(’≥) характеризуЇ, €ка дол€ в≥д вс≥Їњ к≥лькост≥ вим≥рювань буде в≥дпов≥дати значенн€м ’≥.
√раф≥к залежност≥ F(Xi) називають функц≥Їю розпод≥лу ймов≥рностей, тобто величиною, €ка характеризуЇ ймов≥рн≥сть того, що випадкова величина ’ буде знаходитись в д≥апазон≥ [-¥, ’≥].
рива 2 називаЇтьс€ в математиц≥ кривою √аусса, а закон розпод≥лу ймов≥рностей, що описуЇтьс€ ц≥Їю кривою, називаЇтьс€ нормальним або √аусса.
” метролог≥њ вид≥л€ють:
- р≥вном≥рний закон розпод≥лу, граф≥ки €кого мають вигл€д:
 |
–(’≥) –(’≥)
а ’с b ’≥ а b ’≥
–исунок 4.3 Ц √раф≥к р≥вном≥рного закону розпод≥лу.
- трикутний (або —≥мпсона) закон розпод≥лу, граф≥ки €кого мають вигл€д:
 –(’≥) –(’≥)
–(’≥) –(’≥)
0.5
а ’с b ’≥ а ’с b ’≥
–исунок 4.4 Ц √раф≥к трикутного (або —≥мпсона) закону розпод≥лу.






