Производные от некоторых простейших функций

Студенту необходимо научиться вычислять производные конкретных функций: y= x, y= и вообще y = .

Найдем производную функции у=х.

Имеем:

т.е. (x)′=1.

Найдем производную функции

Производная

Пусть тогда

 

Легко заметить закономерность в выражениях производных от степенной функции при n=1,2,3.

Следовательно,

. (1)

Эта формула справедлива для любых действительных n.

В частности, используя формулу (1), имеем:

;

.

 

Пример.

Найдите производную функции

.

Решение:

.

Данная функция является частным случаем функции вида

при .

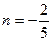Используя формулу (1), имеем

.

 

Производные функций y=sin x и y=cos x.

Пусть y=sinx.

Разделим на ∆x, получим

Переходя к пределу при ∆x→0, имеем

 

Пусть y=cosx.

Тогда

Отсюда

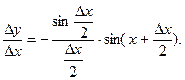
Переходя к пределу при ∆x→0,получим

; . (2)