Погрешности средств измерений. При любом измерении имеется погрешность, представляющая собой отклонение результата измерения от истинного значения измеряемой величины

При любом измерении имеется погрешность, представляющая собой отклонение результата измерения от истинного значения измеряемой величины. На рисунке 1.8 приведена классификация погрешностей средств измерений по ряду признаков.

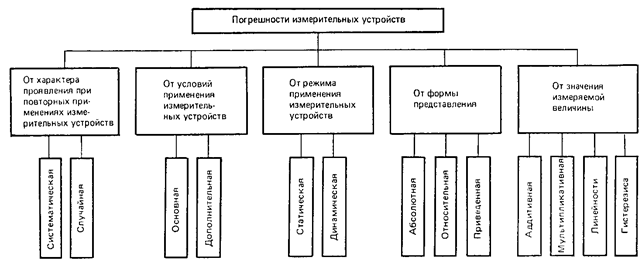
Рис. 1.8. Классификация погрешностей измерительных устройств

Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. По характеру проявления систематические погрешности разделяются на постоянные и переменные. Переменные в свою очередь могут быть прогрессирующими, периодическими и изменяющимися по сложному закону.

Для исключения систематической погрешности наибольшее распространение в практике получил метод поправок.

Случайная составляющая погрешности при повторных измерениях одной и той же величины изменяется случайным образом. Обычно она является следствием одновременного действия многих независимых причин, каждая из которых в отдельности мало влияет на результат измерения. Случайные погрешности не могут быть исключены из результата измерения, но теория вероятности и математическая статистика позволяют оценить результат измерения при наличии случайных погрешностей. Они характеризуются свойствами, которые формулируют двумя аксиомами:

Аксиома случайности — при очень большом числе измерений случайные погрешности, равные по величине и различные по знаку, встречаются одинаково часто. Число отрицательных погрешностей равно числу положительных.
Аксиома распределения — малые погрешности встречаются чаще, чем большие. Очень большие погрешности не встречаются.

Случайные погрешности рассматриваются как случайные величины, подчиняющиеся некоторому симметричному закону распределения.

Основной погрешностью называют погрешность при использовании средства измерений в нормальных условиях. Нормальными условиями применения средств измерений называют условия, при которых влияющие величины имеют номинальные значения или находятся в пределах нормальной области значений. Нормальные условия применения указываются в стандартах или технических условиях на средства измерений. При использовании средств измерений в нормальных условиях считают, что влияющие на них величины практически никак не изменяют их характеристики.

Дополнительной погрешностью измерительного преобразователя (или изменением показаний измерительного прибора) называют изменение его погрешности, вызванной отклонением одной из влияющих величин от ее нормативного значения или выходом ее за пределы нормальной области значений. Дополнительная погрешность может быть вызвана изменением сразу нескольких влияющих величин.

Изменение погрешности, как и других характеристик и параметров измерительных устройств под действием влияющих величин, описывается функциями влияния.

Иными словами, дополнительная погрешность – это часть погрешности, которая добавляется (имеется в виду алгебраическое сложение) к основной в случаях, когда измерительное устройство применяется в рабочих условиях. Рабочие условия обычно таковы, что изменения значений влияющих величин для них существенно больше, чем для нормальных условий, т. е. область рабочих (часть этой области называют расширенной областью) условий включает в себя область нормальных условий.

В некоторых случаях основная погрешность измерительных устройств определяется для рабочей области изменения значений влияющих величин. В этих случаях понятие дополнительной погрешности теряет смысл.

В зависимости от режима применения различают статическую и динамическую погрешности измерительных устройств.

По форме представления принято различать абсолютную, относительную и приведенную погрешности измерительных устройств. У измерительных приборов имеется шкала, отградуированная в единицах входной величины, либо шкала, отградуированная в условных единицах с известным множителем шкалы, поэтому результат измерения представляется в единицах входной величины. Это обусловливает простоту определения погрешности измерительных приборов.

Абсолютной погрешностью измерительного прибора Δ называют разность показаний прибора Х_П и истинного (действительного) Х_Д значения измеряемой величины:

Действительное значение определяется с помощью образцового прибора или воспроизводится мерой.

Относительной погрешностью измерительного прибора называют отношение абсолютной погрешности измерительного прибора к действительному значению измеряемой величины. Относительную погрешность выражают в процентах:

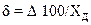Так как Δ << X_Д или Х_П, то в вышеприведенном выражении вместо значения X_Д может быть использовано значение X_П.

Приведенной погрешностью измерительного прибора называют отношение абсолютной погрешности измерительного прибора к нормирующему значению Х_N. Приведенную погрешность также выражают в процентах:

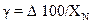В качестве нормирующего значения используется верхний предел измерений, диапазон измерений и др., т. е.

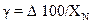Средства измерений могут использоваться в статическом или динамическом режиме работы. В статическом режиме измеряемая величина не изменяется во времени, а отсчет выполняется тогда, когда практически окончены переходные процессы, вызванные подключением измеряемой величины ко входу средства измерений. В динамическом режиме измеряемая величина изменяется во времени. В соответствии с этим различают статическую погрешность средства измерений и погрешность средства измерений в динамическом режиме.

Очевидно, что погрешность средства измерений в динамическом режиме включает в себя статическую погрешность и погрешность, обусловленную инерционностью средства измерений. Последняя погрешность носит название динамической погрешности средства измерений и определяйся как разность между погрешностью средства измерений в динамическом режиме и его статической погрешностью, соответствующей значению величины в данный момент времени.

При анализе погрешностей средств измерений и выборе способов их уменьшения весьма важным является разделение погрешностей по их зависимости от значения измеряемой (преобразуемой) величины. По этому признаку, погрешности делятся на аддитивные, мультипликативные, линейности и гистерезиса.

Аддитивную погрешность иногда называют погрешностью нуля, а мультипликативную – погрешностью чувствительности. Реально погрешность средства измерений включает в себя обе указанные составляющие.

Кроме того, номинальная функция преобразования средства измерений – это в большинстве случаев более простая функция (обычно линейная), чем градуировочная характеристика.

Графически образование перечисленных погрешностей показано на рисунке 1.9.

Рис. 1.9. Реальные функции преобразования измерительных устройств

Аддитивная погрешность постоянна при всех значениях измеряемой величины (рисунок 1.9, а). На рисунке видно, что реальная функция преобразовани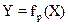я несколько смещена относительно номинальной , т. е. выходной сигнал измерительного устройства при всех значениях измеряемой величины X будет больше (или меньше) на одну и ту же величину, чем он должен быть, в соответствии с номинальной функцией преобразования.

Если аддитивная погрешность является систематической, то она может быть устранена. Для этого в измерительных устройствах обычно имеется специальный настроечный узел (корректор) нулевого значения выходного сигнала.

Если аддитивная погрешность является случайной, то ее нельзя исключить, а реальная функция преобразования смещается по отношению к номинальной во времени произвольным образом. При этом для реальной функции преобразования можно определить некоторую полосу (рисунок 1.9, б), ширина которой остается постоянной при всех значениях измеряемой величины.

Возникновение случайной аддитивной погрешности обычно вызвано трением в опорах, контактными сопротивлениями, дрейфом нуля, шумом и фоном измерительного устройства.

Мультипликативной (получаемой путем умножения), или погрешностью чувствительности измерительных устройств, называют погрешность, которая линейно возрастает (или убывает) с увеличением измеряемой величины.

Графически появление мультипликативной погрешности интерпретируется поворотом реальной функции преобразования относительно номинальной (рисунок 1.9, в). Если мультипликативная погрешность является случайной, то реальная функция преобразования представляется полосой, показанной на рисунке 1.9 (г). Причиной возникновения мультипликативной погрешности обычно является изменение коэффициентов преобразования отдельных элементов и узлов измерительных устройств.

На рисунке 1.9 (д) показано взаимное расположение номинальной и реальной функций преобразования измерительного устройства в случае, когда отличие этих функций вызвано нелинейными эффектами. Если номинальная функция преобразования линейная, то вызванную таким расположением реальной функции преобразования систематическую погрешность называют погрешностью линейности. Причинами данной погрешности могут быть конструкция (схема) измерительного устройства и нелинейные искажения функции преобразования, связанные с несовершенством технологии производства.

Зависимость вход-выход измерительных приборов без учета гистерезиса и ухода нуля может быть представлена в виде:

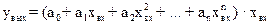где x_вх – измеряемая (входная) величина, y_вых – выходная величина, a₀, a₁, …, a_n – градуировочные коэффициенты.

Реальная функция преобразования может быть представлена линией, примыкающей к прямой a₀x_вх (номинальная функция преобразования) (рисунок 1.10).

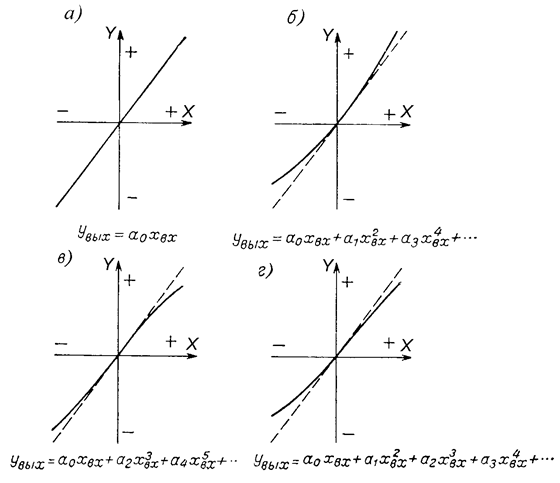
Рис. 1.10. Типичные градуировочные кривые: а – линейная; б – нелинейная при наличии в уравнении преобразования четных степеней x_вх; в - нелинейная при наличии в уравнении преобразования нечетных степеней x_вх; г – нелинейная при наличии в уравнении преобразования четных и нечетных степеней x_вх.

Симметричная кривая (рисунок 1.10, в), описываемая уравнением с нечетными степенями x_вх, наиболее желательна с точки зрения линейности. Как будет показано ниже, нелинейные, но симметричные кривые двух чувствительных элементов, включенных дифференциально, дают улучшение линейности путем исключения членов x_вх с четными степенями.

Наиболее существенной и трудноустранимой систематической погрешностью измерительных устройств является погрешность гистерезиса (от греч. hysteresis – запаздывание), или погрешность обратного хода, выражающаяся в несовпадении реальной функции преобразования измерительного устройства при увеличении (прямой ход) и уменьшении (обратный ход) измеряемой величины (рисунок 1.9, е). Причинами гистерезиса являются: люфт и сухое трение в механических передающих элементах, гистерезисный эффект в ферромагнитных материалах, внутреннее трение в материалах пружин, явление упругого последействия в упругих чувствительных элементах, явление поляризации в электрических, пьезоэлектрических и электрохимических элементах и др. Существенным при этом является тот факт, что форма получаемой петли реальной функции преобразования зависит от предыстории, а именно от значения измеряемой величины, при котором после постепенного увеличения последней начинается ее уменьшение (на рисунке 1.9, е, это показано пунктирными линиями).

В цифровых (ЦИП) квантование по уровню и времени осуществляется путем замены через время Δt (шаг квантования) значений непрерывной функции ближайшим дискретным уровнем с шагом Q. При этом максимальная погрешность от квантования составит
Δ_кв = ± Q/2.

Приведенная погрешность определяется по формуле:

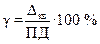где ПД – полный диапазон измеряемой величины.

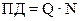где N – число уровней квантования (интервалов).

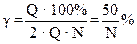Например, измеряет напряжение в диапазоне 0..150 В с γ = 0,1 %. Для определения шага квантования запишем:

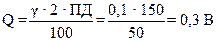Методы повышения точности измерений

Для технологических измерений повышение точности измерений особенно важно в связи с широким применением АСУ ТП. Для решения этой задачи применяются различные методы (рисунок 1.11).

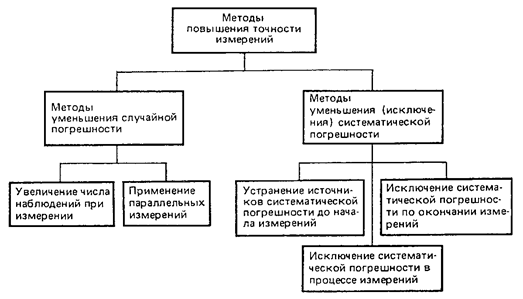
Рис. 1.11. Классификация методов повышения точности измерений

Уменьшения случайной составляющей погрешности измерений увеличивают число наблюдений (см. рисунок 1.10). Оценку среднеквадратического отклонения результата измерения, которая определяет собой случайную погрешность, теоретически можно сделать как угодно малой, увеличив число наблюдений n. Однако на практике в большинстве случаев трудно обеспечить постоянство самого объекта измерений в течение длительного времени, а это может при увеличении числа наблюдений n привести к увеличению погрешности, а не к ее уменьшению.

Другим методом повышения точности измерений за счет уменьшения случайной составляющей погрешности является использование параллельных одновременных измерений одной и той же физической величины. Для этого необходимо использовать сразу несколько средств измерений. Результаты наблюдений, полученных при этих измерениях, обрабатывают совместно. Теоретическая основа этого метода та же, что и предыдущего метода.

Ранее были рассмотрены основные методы исключения систематической погрешности, а именно: методы, основывающиеся на устранении источников систематической погрешности до начала измерений и методы исключения систематических погрешностей по окончании измерений. К числу последних относятся не только применение поправок и поправочных множителей, но и учет дополнительных погрешностей средств измерений.

Кроме этих методов применяют методы, позволяющие определять и исключать систематическую погрешность в процессе измерений. Последние основываются на такой организации процесса измерений и обработки получаемой измерительной информации, которые обеспечивают исключение погрешности или ее определение. Причем применение таких методов возможно и целесообразно в тех случаях, когда известна природа исключаемой систематической погрешности. К числу этих методов относятся: метод замещения, метод компенсации погрешности по знаку и различные методы, базирующиеся на совместных или совокупных измерениях.

При использовании метода компенсации погрешности по знаку процесс измерения организуется таким образом, что известная систематическая погрешность входит в результат каждого из двух повторных измерений с противоположным знаком. Это позволяет после определения среднего арифметического значения исключить систематическую погрешность.

Сущность методов, базирующихся на совместных или совокупных измерениях применительно к уменьшению систематических погрешностей, состоит в том, что в процессе этих измерений изменяют параметр, отвечающий за возникновение систематической погрешности, или осуществляют измерение физической величины совместно и последовательно с несколькими вспомогательными мерами. В результате получают систему независимых уравнений, из решения которой определяют значения измеряемой физической величины уже с учетом систематической погрешности.

Одним из наиболее радикальных путей повышения точности измерений при прочих равных условиях является использование более точных средств измерений. Появление и развитие микроэлектронной техники и микропроцессоров, обеспечивающие возможность практически полной автоматизации самых сложных измерительных процессов, позволили использовать для увеличения точности средств измерений рассмотренные выше методы повышения точности измерений. Наряду с этими методами для повышения точности средств измерений применяется ряд традиционных методов, классификация которых приведена на рисунке 1.12.

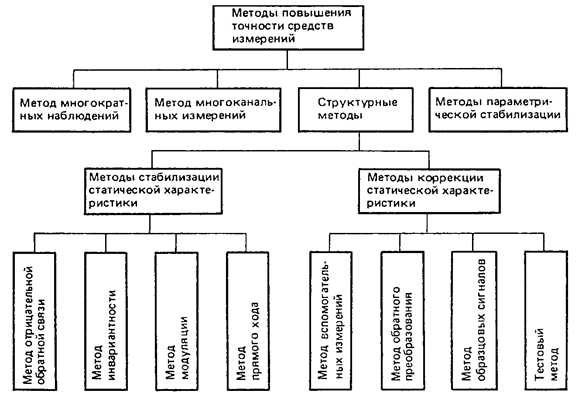
Рис. 1.12. Классификация методов повышения точности средств измерений

Метод многократных наблюдений используется для уменьшения случайной составляющей погрешности средства измерений и состоит в том, что: за некоторый постоянный интервал времени, отведенный для измерения, выполняют несколько наблюдений, затем с помощью вычислительного устройства, входящего в состав данного средства измерений, вычисляют среднее арифметическое значение измеряемой величины и оценку среднеквадратического отклонения результата измерения.

Метод многоканальных измерений аналогичен рассмотренному методу параллельных измерений (см. рисунок 1.12). Средства измерений, с помощью которых реализуется данный метод, содержат несколько идентичных по характеристикам параллельных измерительных цепей (каналов) и вычислительное устройство. Последнее, получая измерительную информацию по этим каналам, вычисляет среднее арифметическое значение измеряемой величины и оценку среднеквадратического отклонения результата измерения. Такой метод позволяет уменьшить случайную составляющую погрешности средства измерений.

Метод параметрической стабилизации, называемый еще конструктивно-технологическим, состоит в стабилизации статической характеристики средств измерений. Параметрическая стабилизация реализуется путем изготовления средств измерений из точных и стабильных элементов, параметры которых мало подвержены внешним влияниям; термостабилизации; стабилизации параметров питания средств измерений; экранировки средств измерений от магнитных и электрических полей и т. п. Данный метод уменьшает систематическую и случайную погрешности средств измерений. Он является классическим в приборостроении. На основе этого метода до сих пор строится современный парк средств измерений.

Структурные методы основаны на том, что в состав средств измерений включаются дополнительные узлы, элементы и меры, обеспечивающие повышение точности этих средств измерений за счет информации, полученной с их помощью. Структурные методы повышения точности средств измерений подразделяют на методы, обеспечивающие стабилизацию статической характеристики средства измерений, и методы, основанные на коррекции этой характеристики.

Структурные методы стабилизации статической характеристики средств измерений (см. рисунок 1.12).

Метод отрицательной обратной связи реализуем только при наличии преобразовательных элементов или преобразователей, способных осуществлять преобразование выходного сигнала средства измерений во входной (обратный преобразователь). Создание таких преобразователей – часто сложная техническая задача. Применение данного метода обеспечивает уменьшение мультипликативной погрешности и погрешности нелинейности, а относительная аддитивная погрешность при этом не изменяется. В то же время использование метода приводит к уменьшению чувствительности средства измерения. Данный метод повышает точность средств измерения и наряду с методом параметрической стабилизации является наиболее распространенным.

Метод инвариантности состоит в том, что в средстве измерений помимо измерительной цепи (канала) имеется сравнительная цепь (канал), к которой не подается входной сигнал, но которая, как и измерительная цепь, находится под воздействием некоторой влияющей величины. Причем параметры сравнительной цепи подобраны так, что изменение ее сигнала под действием влияющей величины идентично изменению сигнала измерительной цепи под действием этой величины, т. е. возмущения, вызванные влияющей величиной, поступают в средство измерений по двум каналам (принцип двухканальности). Использование разности сигналов измерительной и сравнительной цепей (при дифференциальном включении этих цепей) обеспечивает независимость (инвариантность) результирующего сигнала от названной влияющей величины, т. е. метод обеспечивает исключение дополнительной погрешности, вызванной изменениями некоторой, как правило, основной влияющей величины.

Метод модуляции состоит в том, что сигнал, поступающий на вход средства измерений, или параметры этого средства измерений подвергаются принудительным периодическим изменениям (модуляции) с частотой, не совпадающей (обычно более высокой) с областью частот измеряемого сигнала. Использование метода модуляции позволяет уменьшить погрешности от сил трения, явлений поляризации и гистерезиса.

Метод прямого хода состоит в том, что измеряемый сигнал поступает к чувствительному элементу средства измерений через ключ, с помощью которого осуществляется периодическое во времени отключение измеряемого сигнала от чувствительного элемента и подача к последнему сигнала, значение которого равно нулю. Это обеспечивает работу средства измерений на восходящей ветви (прямой ход) статической характеристики при всех значениях измеряемого сигнала, что исключает наиболее существенную погрешность многих средств измерений – погрешность от вариации.

Структурные методы коррекции статической характеристики (методы коррекции погрешности средств измерений). Перечень их приведен на рисунке 1.12.

Метод вспомогательных измерений заключается в автоматизации процесса учета дополнительной погрешности средства измерений по известным функциям влияния ряда влияющих величин. Для этого осуществляется измерение значений этих величин и с помощью вычислительного устройства, построенного с учетом названных функций влияния, автоматически корректируется выходной сигнал средства измерений.

Метод обратного преобразования (итерационный метод) базируется на использовании дополнительно в составе средства измерений кроме прямой измерительной цепи (прямого преобразователя), цепи, способной осуществлять обратное преобразование выходного сигнала (обратный преобразователь), имеющей существенно большую точность, чем цепь прямого преобразования. Результат измерения получают путем итераций. В процессе каждой итерации последовательно осуществляются: прямое преобразование измеряемой величины и запоминание результата, обратное преобразование запомненного значения этой величины, прямое преобразование сигнала обратного преобразователя, соответствующего запомненному значению измеряемой величины, и сравнение результатов этих двух преобразований, на основе которого формируется корректирующий сигнал. Обратный преобразователь в данном методе играет роль как бы многозначной меры, по которой корректируется статическая характеристика прямого преобразователя. Метод обратного преобразования позволяет уменьшать в зависимости от используемого алгоритма коррекции аддитивную и мультипликативную погрешности средств измерений.

Метод образцовых сигналов (образцовых мер) состоит в определении в каждом цикле измерения реальной функции преобразования средства измерений с помощью образцовых сигналов (мер), т. е. метод состоит в автоматической градуировке средства измерений в каждом цикле. Цикл включает в себя измерение физической величины, поступающей на вход средства измерения, поочередное измерение одной или нескольких мер, подключаемых вместо измеряемой физической величины на вход средства измерений, и решение системы уравнений с помощью вычислительного устройства, из которого определяется значение измеряемой физической величины. В этом решении уже учтены изменения реальной статической характеристики, т. е. данный метод сводится к совокупному измерению. Он позволяет уменьшить аддитивную и мультипликативную погрешность, а также погрешность нелинейности.

Тестовый метод сводится к проведению совокупных измерений. В отличие от метода образцовых сигналов в тестовом методе в каждом цикле работы средства измерений кроме измерения физической величины, поступающей на вход средства измерений, осуществляют измерение величин-тестов, каждая из которых формируется из меры и измеряемой величины. Значение измеряемой величины определяется из системы уравнений, решаемой с помощью вычислительного устройства. По существу данный метод является развитием метода образцовых сигналов.