· А)Работа силы.
o Элементарной работой называется скалярное произведение вектора силы на вектор малого перемещения МТ d l*):
. (4.1)
Работа силы на конечном участке траектории 1 – 2 может быть найдена интегрированием вдоль траектории L движения МТ:
. (4.2)
Учитывая связь малого перемещения с мгновенной скоростью МТ d l = V dt, выражение (4.2) может быть записано в виде:
. (4.3)
o Скалярное произведение векторов силы и скорости позволяет определить мощность силы W:
. (4.4)
Очевидно, если векторы F и V перпендикулярны, мощность силы равна нулю, и работа не совершается.
Мощность можно определить и как работу, совершаемую в единицу времени:
. (4.5)
· Если МТ движется по окружности, то элементарная работа, совершаемая при малом угловом перемещении d a:
,
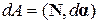
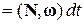а при повороте радиус-вектора на конечный угол:
. (4.6)
· Б) Потенциальная энергия.
o Силы, работа которых не зависит от формы траектории движения МТ, а определяется лишь начальным и конечным положением МТ, называются потенциальными или консервативными. К этому классу относятся гравитационные, упругие и электростатические силы.
Для таких сил работа при перемещении МТ по замкнутой кривой L равно нулю. Математически это можно записать следующим образом:
. (4.7)
Для потенциальных сил можно ввести скалярную функцию координат U (x, y, z), частные производные которой определяют вектор силы F (x, y, z):
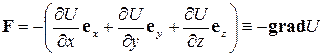. (4.8)
Такая функция U называется потенциальной энергией МТ в поле сил. Работа, совершаемая потенциальной силой при элементарном перемещении МТ, равна:
. (4.9)
Для случая перемещения на конечное расстояние работа потенциальной силы определится через разность потенциальных энергий в начальном и конечном положениях МТ:
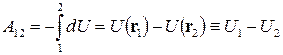. (4.10)
Отметим, что измеряемые в опытах физические величины – сила и работа силы – равны производной и разности значений потенциальной энергии. Следовательно, функция U (x, y, z) определена с точностью до константы. Однако, если принять значение функции U (x, y, z) равным нулю в некоторой точке с координатами x 0, y 0, z 0, то работа, совершаемая силовым полем по перемещению МТ в указанное положение
, (4.11)
будет целиком определяться введенной таким образом функцией U (x, y, z). При этом говорят, что потенциальная энергия нормирована в точке x 0, y 0, z 0.
· В) Кинетическая энергия.
Если сила совершает работу при перемещении МТ под действием только этой силы, то происходит изменение модуля скорости. Можно доказать, что работа равна в этом случае:
. (4.12)
Введем понятие кинетической энергии МТ, определив ее как половину произведения массы точки на квадрат ее скорости:
. (4.13)
Тогда, изменение кинетической энергии МТ движущейся под действием силы определяется работой этой силы (равнодействующей):
. (4.13)
Кинетическую энергию материальной точки можно связать также с её импульсом:
.
Кинетическая энергия – аддитивная величина. Для системы материальных точек:
.
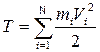Если механическая система представляет собой твердое тело, вращающееся вокруг неподвижной оси OZ, то его полная кинетическая энергия:
, или 
. (4.14)
Если тело совершает плоское движение:
. (4.15)
· Задачи этого раздела, как правило, связаны с нахождением конкретного выражения для потенциальной энергии силового поля или, наоборот, с определением векторной функции F (x, y, z) по известной зависимости потенциальной энергии от координат (формула 4.8).
