Профиль пути синусоидальный

Уравнение вынужденных колебаний подпрыгивания

(1)

Где .

Уравнение подпрыгивания и галопир. идентичны как в левых так и в правых частях, с учетом этого рассмотрим случай колебания подпрыгивания когда профиль пути синусоидальный (i=1), трение в рессорном подвешивании отсутствует ().

Тогда уравнение (1) примет вид

(2).

Решение этого неоднородного уравнения составляет

.

Где - общее решение однород ур-я(без правой части);

- частное решение неоднор уравнен.

Общее решение однор ур-я получим при решении ур-я собствен колебаний без трения:

где Е,φ – амплитуда и нач фаза собственных колебаний, определяемые из нач условия. ω – собственная круговая частота колебаний, рад/с.

Частное решение найдём в форме правой части

,

где М₁ – const подлежащая определению,

р₁ – круговая частота вынужденных колебаний.

Определяем производные и подставим в выражение (2):

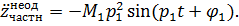
Это уравнение является тождеством, когда + .

Отсюда .

Полное решение всего неоднородного уравнения приобретает вид