1. ¬полне обоснованное изложение рел€тивисткой кинематики отработано на сегодн€ во множестве учебников с разной степенью сложности. Ќе так обстоит дело с динамикой и, тем более, с электродинамикой. ƒл€ строгого изложени€ в теоретической физике в теоретической физике вместо ньютоновской механики используетс€ аналитическа€ механика Ћагранжа и √амильтона, основу которой составл€ет принцип наименьшего действи€. »менно с этих позиций строитс€ четырехмерный вариант теории относительности, более соответствующий ее физической сути, чем представление о раздельном пространстве и времени. ƒл€ ознакомлени€ рекомендуем, например, " урс теоретической физики" Ћ.ƒ.Ћандау, т.1, ћеханика.
Ќа ранних стади€х изучени€ физики такое изложение, конечно, невозможно и тогда приходитс€ допускать некоторое постулирование, которое, впрочем, обычно не вызывает возражени€. Ќапример, зна€ о сущности рел€тивистских преобразований (Ћоренца), удобно начинать с выражений дл€ рел€тивистского импульса и энергии, ввод€ их, как 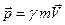 и
и  (здесь
(здесь  Ц то же, что
Ц то же, что  , в любой системе отсчета). ѕри этом уравнение движени€ частицы может быть записано так:
, в любой системе отсчета). ѕри этом уравнение движени€ частицы может быть записано так:
 .
.
Ёто рел€тивистское уравнение вполне применимо дл€ решени€ задач механики, однако дл€ вы€влени€ особенностей теории близкодействи€ его удобно преобразовать, привед€ его к виду классического уравнени€ движени€, где в левой части записываетс€ произведение массы на ускорение.
»спользу€ св€зь энергии и импульса 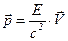 , вместе с выражением дл€ мощности силы
, вместе с выражением дл€ мощности силы  , можно преобразовать левую часть, котора€ сейчас содержит сложную производную:
, можно преобразовать левую часть, котора€ сейчас содержит сложную производную:
 .
.
“еперь уравнение движени€ приобретает классический вид, удобный дл€ решени€ прикладных задач:
 .
.
¬идно, что в услови€х близкодействи€ эффективна€ сила взаимодействи€ (в правой части уравнени€) претерпевает изменени€ по сравнению с классическим случаем, когда ее действие распростран€етс€ мгновенно во всем пространстве. ќтсюда следует известный вывод о неколлинеарности силы и ускорени€ в общем случае. ƒл€ приложений можно провести анализ частных случаев. “ак, дл€ малых скоростей, при  (
( ) получаем
) получаем  и
и  . ѕри умеренных рел€тивистских скорост€х
. ѕри умеренных рел€тивистских скорост€х  , получаем
, получаем  и
и  . ѕри
. ѕри  получаем, аналогично,
получаем, аналогично,  , но
, но  .
.
ќтсюда, в частности, при  получаем
получаем  .
.
«аметим, что второе слагаемое в выражении дл€ эффективной силы пропорционально квадрату скорости, и, подобно в€зкому трению, обеспечивает предельное стационарное значение скорости тела, равное  . “ак, при
. “ак, при  (
( ) взаимодействие прекращаетс€ и
) взаимодействие прекращаетс€ и  . »з последнего, собственно, следует, что в теории дальнодействи€ скорость
. »з последнего, собственно, следует, что в теории дальнодействи€ скорость  €вл€етс€ предельной скоростью осуществлени€ любого взаимодействи€.
€вл€етс€ предельной скоростью осуществлени€ любого взаимодействи€.
“аким образом, в теории относительности сила не €вл€етс€ инвариантной величиной. ѕоперечна€ (относительно направлени€ движени€ инерциальной системы координат) сила преобразуетс€ по формуле  .
.
ƒл€ самой простой ситуации взаимодействи€ двух зар€дов, параллельно движущихс€ со скоростью V относительно неподвижного наблюдател€ Ц все записи скал€рные. ¬ этом случае  и тогда после преобразований нетрудно получить:
и тогда после преобразований нетрудно получить:
|
|
|
 .
.
ѕервое выражение есть электрическа€ составл€юща€, а второе Ц магнитна€.
“еперь, дл€ величины силы можно записать (пренебрега€ малыми величинами в знаменателе):  .
.
«десь  Ц индукци€ магнитного пол€ второго зар€да.
Ц индукци€ магнитного пол€ второго зар€да.






