ўе √≥ппократ в VI стор≥чч€ до н.е. звернув увагу на на€вн≥сть зв'€зку м≥ж статурою ≥ темпераментом людей, м≥ж будовою т≥ла ≥ схильн≥стю до тих або ≥нших захворювань. ѕевн≥ види под≥бного зв'€зку ви€влен≥ також ≥ в тваринному й рослинному св≥т≥. Ќаприклад, в≥домий зв'€зок м≥ж €к≥стю нас≥нн€ ≥ врожайн≥стю культурних рослин. ” рослин ≥ тварин законом≥рност≥ зв'€зк≥в ускладнюютьс€ тим, що зазвичай кожному певному значенню одн≥Їњ з ознак в≥дпов≥даЇ не одне значенн€ ≥ншоњ ознаки, а ц≥ла сукупн≥сть значень. “ак≥ частков≥ зв'€зки м≥ж ознаками, чинниками, под≥€ми, характеристиками називаютьс€ корел€ц≥йними.
1. ѕобудова корел€ц≥йноњ с≥тки ≥ корел€ц≥йноњ таблиц≥. ѕри безпосередньому анал≥з≥ отриманих даних важко скласти €кесь у€вленн€ про на€вн≥сть зв'€заност≥ м≥ж ознаками. Ѕ≥льш €сна картина виходить у тому випадку, €кщо дан≥ табл. 27 в≥добразити граф≥чно, у вигл€д≥ точковоњ д≥аграми (рис. 8). ћ≥сцеположенн€ спостереженн€ визначаЇтьс€ перетином осей абсциси й ординати. “ака систематизац≥€ первинних спостережень вже даЇ в≥доме у€вленн€ про на€вн≥сть корел€тивного зв'€зку. ≤ншим способом зображенн€ корел€ц≥њ Ї складанн€ корел€ц≥йноњ таблиц≥ (або реш≥тки) (табл. 27).
“аблиц€ 27 Ц ƒовжина колоса (’) ≥ число зерен (Y) у рослин €чменю
| є рослини | ’ | Y | є рослини | ’ | Y | є рослини | ’ | Y |
| Ј | Ј | ||||||||||
| ƒовжина колосу (см) | ЈЈ | ||||||||||
| Ј | Ј | Ј | |||||||||
| Ј | ЈЈЈ | ЈЈЈЈ | ЈЈ | ||||||||
| Ј | ЈЈЈ | ЈЈЈЈ | ЈЈЈ | Ј | |||||||
| Ј | ЈЈЈЈ | ЈЈЈ | Ј | Ј | |||||||
| Ј | ЈЈ | ЈЈ | Ј | Ј | |||||||
| Ј | ЈЈ | Ј |
14 16 18 20 22 24 26 28 30 32 34
|
|
|
„исло зерен
–ис. 8 Ц –озпод≥л 50 рослин €чменю за довжиною колоса ≥ числом зерен
” нењ посл≥довно перенос€ть результати первинних спостережень. ћ≥сце кожного спостереженн€ визначаЇтьс€ одночасно за р€дком ’ ≥ графою Y. ѕ≥сл€ перенесенн€ вс≥х даних (дл€ перев≥рки проводитьс€ дв≥ч≥) п≥драховують число точок у кожн≥й кл≥тц≥ ≥ в н≥й же записують результати. ÷≥ числа означають к≥льк≥сть вар≥ант, що мають однакове значенн€ ознак ’ ≥ Y. “ак, число 2 на перетин≥ строки 8 ≥ графи 19 показуЇ, що в дан≥й виб≥рц≥ були 2 рослини, що мали довжину колоса 8 см ≥ 19 зерен у колос≥ (табл. 28).
“аблиц€ 28 Ц орел€ц≥йна таблиц€
| ƒовжина колосу в см (’) | „исло зерен у колос≥ (Y) | —ума за строками fx | ax | fax | fax2 | 
| |||||
| Ј 1 (6) | ЈЈ 2 (3) | Ј 1 (0) | Ц3 | Ц12 | 19,0 | ||||||
| Ј 1 (4) | ЈЈ 2 (2) | ЈЈЈ 3 (0) | Ј 1 (Ц2) | Ц2 | Ц14 | 20,7 | |||||
| Ј 1 (1) | ЈЈЈ 3 (0) | ЈЈЈЈ 4 (Ц1) | ЈЈ 2 (Ц2) | Ц1 | Ц10 | 24,1 | |||||
| ЈЈЈ 3 (0) | ЈЈЈЈЈ 5 (0) | ЈЈЈ 3 (0) | Ј 1 (0) | 25,5 | |||||||
| ЈЈ 2 (1) | ЈЈЈЈЈЈ 6 (2) | ЈЈ 2 (3) | 28,0 | ||||||||
| ЈЈ 2 (4) | Ј 1 (6) | 29,0 | |||||||||
| Ј 1 (6) | Ј 1 (9) | 29,5 | |||||||||
| ЈЈ 2 (12) | 31,0 | ||||||||||
| —ума за графами fy | Ц | Ц6 | |||||||||
| ay | Ц2 | Ц1 | +1 | +2 | +3 | Ц | |||||
| fay | Ц4 | Ц5 | |||||||||
| fay2 |
ѕот≥м п≥драховують частоти кожного р€дка, що даЇ fx ≥ кожноњ графи, що даЇ fy. —уми вс≥х частот, що обчислен≥ окремо за п≥дсумковим р€дком ≥ п≥дсумковою графою, повинн≥ дор≥внювати один одному, вони представл€ють загальне число спостережень (n). ѕри анал≥з≥ ц≥Їњ таблиц≥ видно, що Ї пр€ма корел€ц≥€: у довших колос≥в у середньому б≥льше зерен. ожен горизонтальний ≥ вертикальний р€ди Ї виб≥ркою з нормальним розпод≥лом ознак, що вар≥юють.
Ѕ≥льш рельЇфною ви€вл€Їтьс€ залежн≥сть к≥лькост≥ зерен у колос≥ в≥д його довжини, €кщо з≥ставити зм≥ну довжини колоса з числом зерен у колос≥. ÷≥ дан≥ наведен≥ в стовпц≥  . ” кожному р€дку перемножують число випадк≥в в окрем≥й кл≥тц≥ на в≥дпов≥дне њй значенн€ р€ду Y, сума д≥литьс€ на fx кожного р€дка. Ќаприклад, дл€ першого р€дка: (16Ј1+19Ј2+22Ј1):4=19,0; дл€ другого Ц (16Ј1+19Ј2+22Ј3+25Ј1):7=20,7 ≥ так дал≥. « табл. 28 видно, що в м≥ру зб≥льшенн€ довжини колоса зростаЇ середн€ к≥льк≥сть зерен.
. ” кожному р€дку перемножують число випадк≥в в окрем≥й кл≥тц≥ на в≥дпов≥дне њй значенн€ р€ду Y, сума д≥литьс€ на fx кожного р€дка. Ќаприклад, дл€ першого р€дка: (16Ј1+19Ј2+22Ј1):4=19,0; дл€ другого Ц (16Ј1+19Ј2+22Ј3+25Ј1):7=20,7 ≥ так дал≥. « табл. 28 видно, що в м≥ру зб≥льшенн€ довжини колоса зростаЇ середн€ к≥льк≥сть зерен.
|
|
|
«а пр€моњ л≥н≥йноњ корел€ц≥њ частоти групуютьс€ б≥л€ д≥агонал≥, проведеноњ з л≥вого верхнього до правого нижнього кута. ѕри зворотн≥й Ц з верхнього правого до нижнього л≥вого кута таблиц≥, а середн≥ значенн€ одн≥Їњ ознаки убувають у м≥ру зб≥льшенн€ ≥ншоњ. «а в≥дсутност≥ корел€ц≥њ частоти розташовуютьс€ б≥льш менш р≥вном≥рно, а середнЇ значенн€  ≥
≥  не зм≥нюютьс€ залежно в≥д вар≥юванн€ значень ’ ≥ Y.
не зм≥нюютьс€ залежно в≥д вар≥юванн€ значень ’ ≥ Y.
2. ќбчисленн€ коеф≥ц≥Їнта корел€ц≥њ. оеф≥ц≥Їнт корел€ц≥њ пр€мим способом обчислюють за формулою
 (48)
(48)
ћожна користуватис€ допом≥жними формулами:
 (49)
(49)
 (50)
(50)
 (51)
(51)
«а в≥дсутност≥ корел€ц≥њ, тобто €кщо ознаки вар≥юють незалежно одна в≥д одноњ, будь-€ке ≥з значень  може поЇднуватис€ €к з позитивними, так ≥ з негативними
може поЇднуватис€ €к з позитивними, так ≥ з негативними 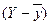 однаково часто. ѕозитивних здобутк≥в
однаково часто. ѕозитивних здобутк≥в 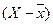
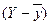 буде ст≥льки ж, ск≥льки ≥ негативних, ≥ сума здобутк≥в буде дор≥внювати або майже дор≥внювати нулю. якщо ознаки вар≥юють зв'€зано, то в≥дхиленн€
буде ст≥льки ж, ск≥льки ≥ негативних, ≥ сума здобутк≥в буде дор≥внювати або майже дор≥внювати нулю. якщо ознаки вар≥юють зв'€зано, то в≥дхиленн€ 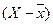 поЇднуватимутьс€ не з будь-€кими, а т≥льки з де€кими в≥дхиленн€ми
поЇднуватимутьс€ не з будь-€кими, а т≥льки з де€кими в≥дхиленн€ми 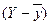 . ѕри пр€м≥й корел€ц≥њ позитивн≥ в≥дхиленн€
. ѕри пр€м≥й корел€ц≥њ позитивн≥ в≥дхиленн€ 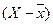 будуть переважно поЇднуватимутьс€ з позитивними, а негативн≥
будуть переважно поЇднуватимутьс€ з позитивними, а негативн≥ 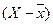 Ц з негативними
Ц з негативними 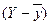 . “обто, здобутки в≥дхилень будуть переважно однозначними, ≥ сума њх Ц позитивною. ѕри зворотн≥й корел€ц≥њ поЇднуютьс€ переважно в≥дхиленн€ з р≥зними знаками, ≥ сума њх здобутк≥в буде негативна. ≤ в тому ≥ в ≥ншому випадку сума здобутк≥в буде тим б≥льше, чим менше буде незалежних поЇднань в≥дхилень, тобто чим б≥льше буде спр€жен≥сть м≥ж ознаками, що вар≥юють.
. “обто, здобутки в≥дхилень будуть переважно однозначними, ≥ сума њх Ц позитивною. ѕри зворотн≥й корел€ц≥њ поЇднуютьс€ переважно в≥дхиленн€ з р≥зними знаками, ≥ сума њх здобутк≥в буде негативна. ≤ в тому ≥ в ≥ншому випадку сума здобутк≥в буде тим б≥льше, чим менше буде незалежних поЇднань в≥дхилень, тобто чим б≥льше буде спр€жен≥сть м≥ж ознаками, що вар≥юють.
ѕри обробц≥ нечисленноњ виб≥рки можна скористатис€ формулою (52):
 (52)
(52)
ћожна скористатис€ способом Ђдов≥льного початкуї (непр€мий спос≥б):
 (53)
(53)
де ах ≥ ау Ц в≥дхиленн€ значень X ≥ Y в≥д свого дов≥льного початку в одиниц€х ≥нтервалу; f Ц частота в≥дпов≥дних груп.
оеф≥ц≥Їнт корел€ц≥њ може набувати значень в≥д +1 до Ц1, залежно в≥д т≥сноти зв'€зку. ѕри повн≥й пр€м≥й корел€ц≥њ r=+1, при повн≥й зворотн≥й r=Ц1. оли корел€ц≥€ в≥дсутн€, коеф≥ц≥Їнт близький до 0. «азвичай вважають, що величина r=0,20Ц0,30 св≥дчить про на€вн≥сть слабкоњ, r=0,50Ц0,60 Ц середньоњ, а r=0,80Ц0,90 Ц сильноњ (т≥сноњ) корел€ц≥њ м≥ж ознаками.
3. ќбчисленн€ квадратичноњ помилки коеф≥ц≥Їнта корел€ц≥њ. «а умов, €кщо виб≥рка проведена з нормальноњ сукупност≥, помилку коеф≥ц≥Їнта корел€ц≥њ обчислюють за формулою (54):
 (54)
(54)
4. ќц≥нка ≥стотност≥ коеф≥ц≥Їнта корел€ц≥њ. оеф≥ц≥Їнт корел€ц≥њ вважають за ≥стотний, €кщо в≥рог≥дн≥сть по€ви такоњ корел€ц≥њ в св≥домо некорел€тивн≥й сукупност≥ буде дуже мала. “аким чином, завданн€ зводитьс€ до оц≥нки значущост≥ в≥дхилень r в≥д нул€. ѕри великому числ≥ спостережень (n≥30) коеф≥ц≥Їнт корел€ц≥њ можна вважати за ≥стотний, €кщо в≥н перевищуЇ свою помилку в 3 ≥ б≥льше раз≥в, тобто  . ” нечисленних виб≥рках ≥стотн≥сть коеф≥ц≥Їнта корел€ц≥њ оц≥нюЇтьс€ за допомогою критер≥ю t:
. ” нечисленних виб≥рках ≥стотн≥сть коеф≥ц≥Їнта корел€ц≥њ оц≥нюЇтьс€ за допомогою критер≥ю t:
 (55)
(55)
де n Ц число парних спостережень.
«≥ставленн€ фактичного ≥ табличного t при числ≥ ступен≥в свободи k=nЦ1 даЇ можливим оц≥нити ≥стотн≥сть r при вибраному р≥вн≥ значущост≥.
5. —пос≥б обчисленн€ коеф≥ц≥Їнта корел€ц≥њ за допомогою дов≥льного початку. ќтриман≥ дан≥ групують у корел€ц≥йну таблицю. «а дов≥льний початок в≥дл≥ку беруть значенн€ ’ ≥ Y, що знаход€тьс€ в середин≥ р€ду. Ќаприклад, јх=10, јy=22. –€док ≥ графу в≥дкреслюють жирними або кольоровими л≥н≥€ми. ¬иходить 4 квадранта. ѕот≥м обчислюють в≥дхиленн€ значень ≥нтервальних груп в≥д своњх ј, записують њх в р€док ах ≥ ау. ќбчислюють fax, fax2, fay, fay2.
ѕ≥сл€ цього обчислюють здобутки axay дл€ кожноњ кл≥тки корел€ц≥йноњ таблиц≥. Ќаприклад, дл€ першоњ кл≥тки верхнього р€дка axay=(Ц3)(Ц2)=6 ≥ так дал≥. ÷≥ здобутки записують в тих же кл≥тках кольоровим ол≥вцем або беруть у дужки. ѕот≥м п≥драховують суму вс≥х faxay, враховуючи знаки. “аблицю краще розд≥лити на 4 квадранти. axay кожного квадранта таблиц≥ мають певн≥ знаки: плюс Ц в л≥вому верхньому (I) ≥ правому нижньому (III), м≥нус Ц в правому верхньому (II) ≥ л≥вому нижньому куту (IV).
|
|
|
I квадранта = 1Ј6+2Ј3+1Ј4+2Ј2+1Ј1=21
II квадранта = 1Ј(-2)+4Ј(-1)+2Ј(-2)= Ц10
III квадранта = 0
IV квадранта = 2Ј1+6Ј2+2Ј3+..+2Ј12=73 –азом = 84
ќтже, 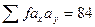 ;
;  ;
;  ;
;  ;
;  ;
;  ; n=50
; n=50
 .
.
ƒал≥ проводитьс€ оц≥нка ≥стотност≥ коеф≥ц≥Їнта корел€ц≥њ.
6. ќбчисленн€ корел€ц≥йного в≥дношенн€. ” тих випадках, коли попередн≥й анал≥з показуЇ, що залежн≥сть м≥ж двома ознаками маЇ кривол≥н≥йних характер, коеф≥ц≥Їнт корел€ц≥њ не даЇ повного у€вленн€ про ступ≥нь зв'€зку м≥ж ознаками. ¬ цьому випадку обчислюють показник кривол≥н≥йноњ залежност≥, так зване корел€ц≥йне в≥дношенн€ η (ета), що Ї в≥дношенн€м двох дисперс≥й: дисперс≥њ групових середн≥х ≥ загальн≥й дисперс≥њ. “обто корел€ц≥йне в≥дношенн€ в≥дпов≥даЇ на питанн€: €ку частину загальноњ дисперс≥њ результативноњ ознаки складаЇ дисперс≥€ приватних середн≥х ц≥Їњ ознаки. орел€ц≥йне в≥дношенн€ обчислюЇтьс€ за формулою (56):
 (56)
(56)
де  Ц середнЇ в≥дношенн€ групових середн≥х;
Ц середнЇ в≥дношенн€ групових середн≥х;  Ц середнЇ квадратичне в≥дхиленн€ Y.
Ц середнЇ квадратичне в≥дхиленн€ Y.
орел€ц≥йне в≥дношенн€ завжди позитивно ≥ набуваЇ значень в≥д 0 до 1. ” раз≥ пр€мол≥н≥йного зв'€зку коеф≥ц≥Їнт корел€ц≥њ (його абсолютна величина) ≥ корел€ц≥йне в≥дношенн€ р≥вн≥. якщо зв'€зок кривол≥н≥йний, то η>r.
ѕриклад. ” табл. 29 наведен≥ дан≥ про залежн≥сть м≥ж вм≥стом жиру ≥ йодним числом у 296 зразк≥в соњ. r=Ц0,100, отже зв'€зок м≥ж цими ознаками в≥дсутн≥й. ¬ той же час характер зм≥н йодного числа вказуЇ на на€вн≥сть кривол≥н≥йноњ залежност≥: ≥з зб≥льшенн€м вм≥сту жиру йодне число спочатку зменшуЇтьс€ з 137 до 126, а пот≥м знов зб≥льшуЇтьс€ до 131.
“аблиц€ 29 Ц «алежн≥сть м≥ж вм≥стом жиру ≥ йодним числом у нас≥нн≥ соњ
| % жиру ’ | …одне число  (групова середн€) (групова середн€)
| fy | 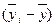
| 
| 
|
| 9,1 | 82,81 | 165,62 | |||
| 7,1 | 50,41 | 504,10 | |||
| 3,1 | 9,61 | 182,59 | |||
| Ц1,9 | 3,61 | 245,48 | |||
| Ц1,9 | 3,61 | 274,36 | |||
| 1,1 | 1,21 | 79,86 | |||
| 1,1 | 1,21 | 53,24 | |||
| 2,1 | 4,41 | 30,87 | |||
| 3,1 | 9,61 | 38,44 | |||
| Cума | 1574,56 |
ƒл€ обчисленн€ корел€ц≥йного в≥дношенн€:
1) знаход€ть середнЇ виб≥рки:  одиниц≥;
одиниц≥;
2) обчислюють в≥дхиленн€ групових середн≥х в≥д загальноњ середньоњ, тобто 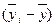 ;
;
3) квадрати в≥дхилень помножають на частоту fy;
4) обчислюють середнЇ квадратичне в≥дхиленн€ групових середн≥х
 ;
;
5) обчислюють звичайним способом (тут не приводитьс€) σy=4,78 одиниц≥;
6) знаход€ть корел€ц≥йне в≥дношенн€

вадратична помилка корел€ц≥йного в≥дношенн€ може бути обчислена за наближеною формулою (57):
 (57)
(57)
” даному приклад≥ 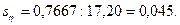 « достатньою достов≥рн≥стю можна вважати корел€ц≥йне в≥дношенн€ ≥стотним, коли воно перевершуЇ свою помилку в 3 ≥ б≥льше раз≥в, тобто коли
« достатньою достов≥рн≥стю можна вважати корел€ц≥йне в≥дношенн€ ≥стотним, коли воно перевершуЇ свою помилку в 3 ≥ б≥льше раз≥в, тобто коли 
7. ќбчисленн€ критер≥ю кривол≥н≥йност≥. ѕри корел€ц≥йному анал≥з≥ характер зв'€зку м≥ж ознаками часто вдаЇтьс€ визначити за зм≥ною групових середн≥х. Ѕ≥льш менш правильна, систематична зм≥на њх в≥д групи до групи (тобто зб≥льшенн€ або зменшенн€) вказуЇ на на€вн≥сть л≥н≥йноњ залежност≥. ” таких випадках необх≥дн≥сть в обчисленн≥ њх в≥дпадаЇ.
« ≥ншого боку, €кщо характер зм≥ни групових середн≥х вказуЇ на кривол≥н≥йну залежн≥сть, тод≥ дл€ характеристики т≥сноти зв'€зку обчислюють корел€ц≥йне в≥дношенн€. ѕроте в де€ких випадках за зм≥ною групових середн≥х важко судити за характером зв'€зку ≥ доводитьс€ обчислювати обидва показники Ц коеф≥ц≥Їнт корел€ц≥њ ≥ корел€ц≥йне в≥дношенн€.
ƒе€ке у€вленн€ про характер зв'€зку даЇ р≥зницю ηЦr; чим вона б≥льша, тим, взагал≥ кажучи, Ђб≥льш кривол≥н≥йнаї залежн≥сть м≥ж ознаками. јле оск≥льки ц≥ обидва коеф≥ц≥Їнти, €к ≥ будь-€ка ≥нша статистична характеристика, схильн≥ до випадкових коливань, €к≥ можуть бути одно- ≥ р≥знозначними, необх≥дно у кожному окремому випадку об'Їктивно оц≥нити, наск≥льки η в≥др≥зн€Їтьс€ в≥д r, ≥накше кажучи, визначити можлив≥ меж≥ випадкових коливанн≥ р≥зниц≥ ηЦr. “аку перев≥рку провод€ть за допомогою критер≥ю кривол≥н≥йност≥, користуючись в≥домим прийомом знаходженн€ в≥дношенн€
|
|
|
 (58)
(58)
„исельником ц≥Їњ формули Ї р≥зниц€ квадрат≥в, а знаменником Ц помилка ц≥Їњ р≥зниц≥, що обчислюЇтьс€ за формулою:
 (59)
(59)
–озраховану за формулою (58) величину t пор≥внюють з табличним њњ значенн€м при вибраному р≥вн≥ значущост≥ ≥ числ≥ ступен≥в свободи, що дор≥внюЇ nЦ2. –≥зниц€ ηЦr вважаЇтьс€ за ≥стотну, €кщо tфакт дор≥внюЇ або б≥льше tтабл. ¬ цьому випадку визнають, що зв'€зок м≥ж ознаками ≥стотно кривол≥н≥йний.
ѕриклад. ѕри перев≥рц≥ кривол≥н≥йност≥ зв'€зку м≥ж вм≥стом жиру в нас≥нн≥ соњ та йодним числом отриман≥ наступн≥ дан≥: η =0,483; r= 0,100, n=296, η2Цr2=0,2233.
ќбчислюЇмо помилку р≥зниц≥ sηЦr за формулою (59):
 ;
;  .
.
8. –озрахунок коеф≥ц≥Їнта детерм≥нац≥њ. ƒл€ тлумаченн€ значень, що Ї показниками т≥сноти корел€ц≥йного зв'€зку, використовують так зван≥ коеф≥ц≥Їнти детерм≥нац≥њ, €к≥ показують, €ка частка вар≥ац≥њ одн≥Їњ ознаки залежить в≥д вар≥юванн€ ≥ншоњ ознаки. «а на€вност≥ л≥н≥йного зв'€зку коеф≥ц≥Їнт детерм≥нац≥њ Ї квадратом коеф≥ц≥Їнта корел€ц≥њ  , а за нел≥н≥йноњ залежност≥ м≥ж ознаками ’ ≥ Y Ц квадрат корел€ц≥йного в≥дношенн€
, а за нел≥н≥йноњ залежност≥ м≥ж ознаками ’ ≥ Y Ц квадрат корел€ц≥йного в≥дношенн€  . “ак, коеф≥ц≥Їнт детерм≥нац≥њ м≥ж (’) надземною ≥ п≥дземною масою (Y) частини рослин складаЇ
. “ак, коеф≥ц≥Їнт детерм≥нац≥њ м≥ж (’) надземною ≥ п≥дземною масою (Y) частини рослин складаЇ  або 27,4 %. ÷е означаЇ, що лише 27,4 % вар≥ац≥њ ознаки ’ визначаЇтьс€ вар≥юванн€м ознаки Y. Ќайчаст≥ше застосовують квадрат корел€ц≥йного в≥дношенн€.
або 27,4 %. ÷е означаЇ, що лише 27,4 % вар≥ац≥њ ознаки ’ визначаЇтьс€ вар≥юванн€м ознаки Y. Ќайчаст≥ше застосовують квадрат корел€ц≥йного в≥дношенн€.
оеф≥ц≥Їнт детерм≥нац≥њ даЇ п≥дставу побудувати наступну зразкову шкалу, що дозвол€Ї робити висновок про т≥сноту зв'€зку м≥ж ознаками: при r=0,5Ц0,6 зв'€зок вважаЇтьс€ за середн≥й, r<0,5 вказуЇ на слабкий зв'€зок ≥ лише при r≥0,7 можна судити про сильний зв'€зок, коли приблизно 50 % вар≥ац≥њ ознаки Y залежить в≥д вар≥ац≥њ ознаки ’.






