Числа Мерсенна — числа вида 
, где 
— простое число.
Числа Вудалла — числа вида 
, где 
— натуральное число.
Числа Прота — числа вида 
, где — натуральное число, а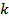 
нечетно и 
.
Числа Кулдена — числа вида 
, где — натуральное число. При 
числа Кулдена являются частным случаем чисел Прота.
Числа Ферма — числа вида 
, где — целое положительное число. Числа Ферма являются частным случаем чисел Прота при 
и 
. По состоянию на ноябрь 2011 года известно только 5 простых чисел Ферма для 
и высказана гипотеза, что других простых чисел Ферма нет.
Принято отмечать наибольшие простые числа. Один из рекордов поставил в свое время Эйлер (1707-1783), найдя простое число 
. По состоянию на ноябрь 2011 года наибольшим простым числом является 
. Оно относится к числам Мерсенна и содержит 12 978 189 десятичных цифр.
