‘ормулы включени€-исключени€ позвол€ют определить число элементов в объединении нескольких конечных множеств. –ассмотрим случаи двух и трех множеств. „исло элементов конечного множества будем обозначать через 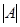 .
.
“огда дл€ двух конечных множеств ј и ¬ справедлива формула,

| (7.1) |
—праведливость этой формулы можно проиллюстрировать диаграммой Ёйлера-¬енна.
| ƒействительно общее количество элементов в объединении двух множеств будет складыватьс€ из количества элементов в области ј и из количества элементов в области ¬ без двойного подсчета элементов в пересечении двух областей (заштрихованна€ область) | 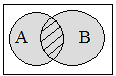
|
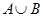
|
ƒл€ трех конечных множеств ј, ¬ и — справедлива формула
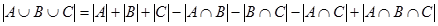
| (7.2) |
| ќбщее количество элементов в объединении трех множеств будет складыватьс€ из количества элементов в области ј, из количества элементов в области и ¬ количества элементов в области — без двойного подсчета элементов в пересечении пар областей (заштрихованна€ область), но с учетом области тройного наложени€. | 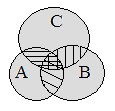
|
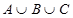
|
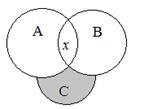
ѕример 1.14. ѕорезультатам тестов из 25 слушателей студенческой группы 12 человек показали себ€ как обладатели веселого характера, 16 Ч про€вили себ€ как замкнутые и 8 не показали себ€ ни веселыми, ни замкнутыми. —колько человек оказались одновременно веселого, но не замкнутого характера?
–ешение. ѕусть ј Ч множество студентов веселого характера, ¬ Ч множество студентов замкнутого характера, и — Ч множество студентов не обладающих ни веселым ни замкнутым характером.
оличество студентов, которые имеют либо веселый, либо замкнутый характер, равно 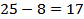 . ќбозначим через . ќбозначим через  количество студентов веселого, но не замкнутого характера, тогда количество студентов веселого, но не замкнутого характера, тогда 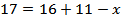 . ќтсюда . ќтсюда 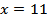 . .
| 
|
ѕример 1.14. ¬ бюро переводов работают несколько человек, причем каждый из них знает хот€ бы один из трех €зыков Ч английский, французский и немецкий. јнглийский €зык знают 12 человек, французский Ч 10 человек, немецкий Ч 8 человек, английский и французский Ч 6 человек, английский и немецкий Ч 4 человека и французский и немецкий Ч 2 человека. ¬се три €зыка знает один человек. —колько человек работает в бюро переводов? —колько из них знает только английский €зык? “олько французский €зык? “олько немецкий €зык?
–ешение. ¬ведем следующие множества:
ј Ч множество всех сотрудников, знающих английский €зык;
¬ Ч множество всех сотрудников, знающих французский €зык;
— Ч множество всех сотрудников, знающих немецкий €зык,
D Ч множество всех сотрудников, знающих английский и французский €зыки,
E Ч множество всех сотрудников, знающих английский и немецкий €зыки.
»з услови€ задачи можно записать:
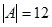 , , 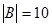 , , 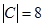
| 
|
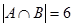 , ,  , , 
| |
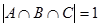
|
ѕримен€€ формулу включени€-исключени€ дл€ трех множеств, получим общее число переводчиков бюро:
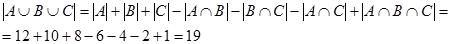
|
ѕродолжим вычислени€:
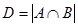 , , 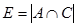 , , 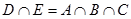
| |
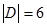 , , 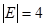 , , 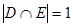
|
ѕрименим формулу включени€-исключени€ дл€ двух множеств получим
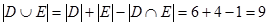
|
»так, английский €зык знают 12 человек, из них еще хот€ бы один €зык знают 9 человек. ѕоэтому только английский знают 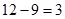 человека.
человека.
|
|
|
јналогично находим, что французский €зык и еще хот€ бы один €зык знают 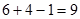 человек. ѕоэтому число сотрудников, знающих только французский равно
человек. ѕоэтому число сотрудников, знающих только французский равно 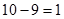 .
.
“олько немецкий €зык знают 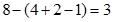 человек.
человек.






