¬ испытательной лаборатории при предпри€тии, выпускающем силомеры, в процессе длительных экспериментальных и научных изысканий была создана физико-математическа€ модель удара человека по упругой мишени. — помощью этой модели можно точно описать и пон€ть весь процесс соударени€ и объ€снить форму ударного импульса.
¬ качестве модели бьющего человека беретс€ система трех тел, лет€щих друг за другом и имеющих между собой упругую св€зь K1 и K2. ѕервое тело массой m Ц это кисть с предплечьем (до локтевого сустава) или стопа с голенью. ¬торое тело массой m1 Ц это плечо или бедро. “ретье тело массой m2 Ц это часть массы туловища, участвующа€ в ударе. ¬ момент удара силой мышц человека создаетс€ жестка€ упруга€ св€зь K2, благодар€ которой медленна€, но относительно больша€ масса m2 поможет сначала разогнать до максимальных скоростей бьющую конечность, а затем и примет непосредственное участие в ударе, передава€ свой импульс и энергию мишени.
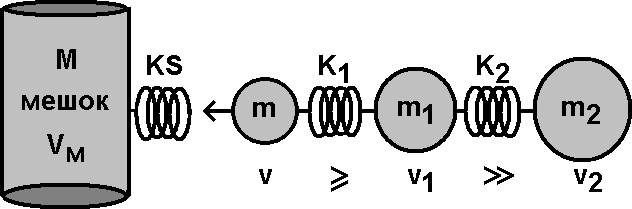
–ис. 1. ћодель человека, бьющего по упругому мешку.
¬ зависимости от жесткости св€зи K1 по€вл€ютс€ два варианта развити€ событий, которые определ€ют два типа ударов в боксе Ц пр€мой и боковой.
”пругую поверхность мишени можно представить как покрытие, состо€щее из множества пружинок жесткостью K0. “огда закон √ука при площади ударной поверхности S примет вид:
F = nK0X = SXK0/S0 = SXK = KSX
«десь n Ц количество пружинок на площади S; S0 Ц площадь, занимаема€ одной пружинкой; X Ц величина деформации; K = K0/S0 Ц жесткость на единицу площади (удельна€ жесткость поверхности). »звестно, что столкновение тела массой m с упругой стенкой можно описать дифференциальным уравнением гармонических колебаний
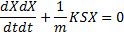
¬ случае столкновени€ двух тел массами m и M уравнение примет вид:
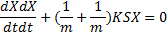
или, в общем виде,
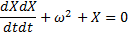
где

–ешение этого уравнени€ при заданных начальных услови€х (при t = 0, dX/dt = v) известно:
X = (v/ 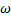 ) sin(
) sin(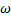 t).
t).
ћаксимальное значение F (сила удара) в этом случае будет равна
Fmax = KSXmax = KSv/ 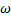 ,
,
а врем€ соударени€ T = /. ѕолучаем две важные формулы:
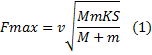
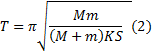
«амечание. формулы (1) и (2) получены дл€ идеального случа€, когда ударна€ воронка на поверхности мишени имеет цилиндрическую форму. ќднако на практике ударна€ воронка имеет более сложные формы. ¬виду этого формула (1) дл€ расчета силы удара имеет вид
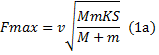
¬еличина C измен€етс€ от 0 (всегда больше нул€) до 1, и в случае с идеальной цилиндрической воронкой равна 1. ƒл€ других форм воронок она может быть вычислена исход€ из того, что при M>>m в момент возникновени€ максимальной силы удара потенциальна€ энерги€ всех сжатых пружин воронки (она рассчитываетс€ как сумма потенциальных энергий всех пружин, кажда€ из которых сжимаетс€ по-разному в зависимости от формы ударного тела) равна исходной кинетической энергии ударного тела. ќтсюда можно найти максимальную глубину воронки, а затем и суммарную силу (как сумму сил сжати€ всех пружин). оэффициент C при этом стоит в подкоренном выражении, как в формуле (1a). “ак, например, рассчитано, что дл€ воронки в форме правильного конуса C = 2/3, дл€ правильного полушара C = 8/9. ”читыва€, что эта величина стоит под корнем, можно утверждать, что форма воронки сказываетс€ на силе удара не столь значительно. ѕоэтому дальнейшие рассуждени€ дл€ простоты продолжим дл€ идеальной цилиндрической ударной воронки.
|
|
|
ѕеремножа€ формулы (1) и (2), получаем третье соотношение:
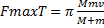 (3)
(3)
или

где – Ц импульс мешка при упругом столкновении:
P = 2FmaxT/  (4)
(4)
–азделив друг на друга формулы (1) и (2), получим еще одно соотношение:
Fmax = KSTv/  (5)
(5)
‘ормула (1) объ€сн€ет, что сила удара зависит от скорости ударной конечности, ее размеров и массы, а также от массы и жесткости мешка.
≈сли M>5m, то дл€ всех мешков массой от 5m до бесконечности сила удара не изменитс€ более чем на 10% (при одинаковых параметрах ударной конечности). ѕри изменении жесткости мешка в пределах 20% сила удара мен€етс€ не более чем на 10%. ѕри увеличении жесткости мешка более чем на 20% существенно возрастает веро€тность травматизма при ударах рукой. ƒл€ ударов ногой жесткость мешка можно подн€ть на 50Ц70%. ¬ этом случае сила удара возрастает на 25Ц30%. ¬ зависимости от весовой категории спортсмена сила удара за счет размеров и массы ударной конечности может различатьс€ более чем в 2 раза.
— помощью формулы (2), измер€€ врем€ соударени€, можно вычислить жесткость мешка KS и его удельную жесткость K.
ѕо формуле (5), зна€ силу удара, врем€ соударени€ и жесткость мешка, можно оценить скорость ударной конечности в момент удара. —корость ударной конечности можно также определить и из формулы (3), зна€ импульс мешка (силу удара и врем€ соударени€), его массу и массу ударной конечности.
–ассмотрим форму ударного импульса бокового и пр€мого удара профессионала (р€д 1, 2) и любител€ (р€д 3, 4):
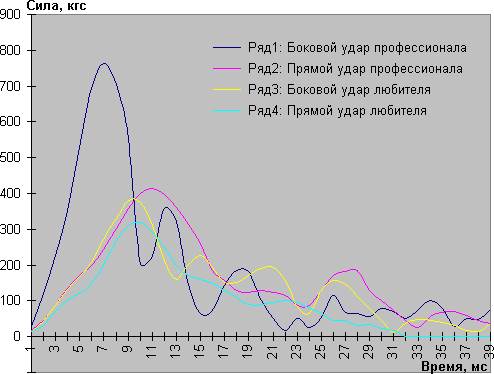
–ис. 2. ‘ормы ударных импульсов дл€ различных ударов и спортсменов.
–азложим графически боковой и пр€мой удар боксера на составл€ющие, чтобы оценить вклад каждого тела в удар. ѕолучим следующие графики:
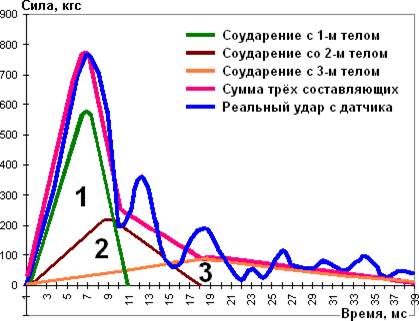
–ис. 3. –азложение на составл€ющие бокового удара профессионального боксера.
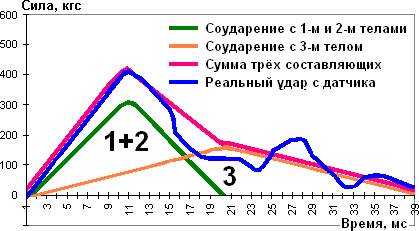
–ис. 4. –азложение на составл€ющие пр€мого удара профессионального боксера.
»з графиков ударов и вышеприведенных формул можно сделать следующие выводы:
1. ¬рем€ нарастани€ удара t определ€етс€ только массами первого и второго тела и жесткостью св€зи между ними. “ретье тело на t вли€ть не может.
2. ѕри пр€мом ударе профессионала врем€ нарастани€ удара t максимально и составл€ет примерно 10 мс. Ёто означает присутствие жесткой св€зи между первым и вторым телом в момент удара. ѕервое и второе тело ведут себ€ как единое целое массой (m+m1). ¬рем€ t максимально.
3. ѕри боковом ударе упруга€ св€зь между первым и вторым телом становитс€ значительно слабее, и сила удара на 80% определ€етс€ ударом первого тела. ѕри этом врем€ нарастани€ удара t уменьшаетс€ в полтора раза (так как m и m1 примерно равны). “ак как упругость св€зи между первым и вторым телом становитс€ сравнима с упругостью мешка, на графике ударного импульса наблюдаетс€ картина затухающих биений.
4. «на€ из графика врем€ нарастани€ удара, можно оценить удельную жесткость мешка:

ѕри массе руки m = 2 кг, площади ударной поверхности кулака S = 40Ц45 см2 и времени соударени€ “ = 2t = 0,012 с (t = 6 мс Ц врем€ нарастани€ удара) значение K составл€ет 3000 кг/(с2Хсм2).
|
|
|
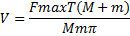
5. ” профессионала скорость кулака при боковом ударе более чем в два раза выше, чем при пр€мом. “ак как, согласно формуле (3),
то, учитыва€ вклад в силу каждого тела, получаем в случае пр€мого удара v = 5,5 м/с, а при боковом ударе Ц v = 12 м/с.
6. ¬клад третьего тела в значение максимальной силы удара незначителен Ц 10Ц15%. ќднако велик его вклад в импульс и в энергию удара: вклад в импульс Ц до 50% при боковом ударе и до 100% при пр€мом. —оответственно, прирост энергии удара за счет третьего тела увеличиваетс€ при боковом ударе более чем в два раза и более чем в три раза при пр€мом.
јнализиру€ видео-ролик на странице Ђ“ренажер в действииї, также легко пон€ть, что сила удара пропорциональна общему времени соударени€ (дл€ конкретного вида ударов). Ќо врем€ соударени€ пропорционально ударной массе. ќтсюда вывод Ц максимальную скорость удар€ющей конечности, котора€ определит рекордную силу удара, можно получить, только подключив при ударе как можно большую массу тела.
7. »з графиков видно, что при боковом ударе из-за слабой св€зи K1 вклад третьего тела в импульс и энергию удара существенно ниже, чем при пр€мом, но все это с успехом компенсируетс€ вторым телом. »мпульс же, сообщенный мешку при боковом ударе первым телом, практически оказалс€ равным импульсу от тела, образованного первым и вторым при пр€мом ударе. “аким образом, максимальные значени€ импульса и энергии пр€мых и боковых ударов отличаютс€ несущественно.
8. «на€ зависимость времени соударени€ от ударной массы, можно оценить массу третьего тела, участвующего в ударе. ѕри общем времени соударени€ 40 мс это будет примерно 28 кг. ј обща€ задействованна€ при ударах рукой масса в данном случае составл€ет не менее 32 кг (50% массы спортсмена).
9. јнализиру€ удары, видно, что пр€мой и боковые удары любител€ совсем мало отличаетс€ друг от друга. ќни как бы занимают промежуточные значени€ между правильными пр€мым и боковым ударами профессионала. ѕри этом у любителей легких весовых категорий пр€мые и боковые удары смещены в сторону правильного бокового удара (недостаточно жесткости при нанесении пр€мых ударов), а у любителей средней весовой категории наблюдаетс€ смещение в сторону пр€мого удара (избыточна€ жесткость при нанесении боковых ударов).
10. ќказалось, что скорость нарастани€ удара (она пропорциональна силе удара и скорости ударной конечности) сильно зависит от типа удара и его правильности. ѕоэтому контролировать правильность удара проще всего, анализиру€ врем€ нарастани€ ударного импульса, так как оно не зависит от скорости и силы удара.
≈сли выводить на индикацию само врем€ нарастани€ удара, то дл€ правильных боковых ударов оно должно быть минимально, а дл€ правильных пр€мых наоборот максимально. –азличие это должно составл€ть 40Ц60%.






