
аждое из рассматриваемых здесь дифференциальных уравнений представл€ет собой закон сохранени€ какой-либо физической величины. ќбычно зависимыми переменными в этих дифференциальных уравнени€х €вл€ютс€ удельные свойства, т.е. отнесенные к единице массы. ѕримерами €вл€ютс€ массова€ концентраци€, скорость, удельна€ энтальпи€.
¬опрос: кака€ величина не €вл€етс€ удельным свойством, но котора€ часто используетс€?
„лены дифференциального уравнени€ такого типа выражают воздействие на единицу объема. ѕусть  поток некоторой переменной ‘.
поток некоторой переменной ‘.
–ассмотрим объем

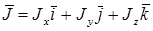
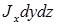 - поток, втекающий через грань
- поток, втекающий через грань
 - вытекающий поток
- вытекающий поток
–азность между втекающим и вытекающим потоком:
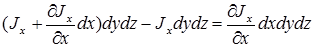
јналогично дл€ двух других осей можем получить 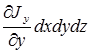 ,
, 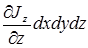 . «амеча€ что
. «амеча€ что 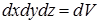 - объем, получим чистое истечение на единицу объема
- объем, получим чистое истечение на единицу объема

“ака€ интерпретаци€ 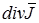 особенно полезна ввиду того, что, как будет видно ниже, построение численного метода будет выполн€тьс€ на основе принципа баланса дл€ контрольного объема. единице объема относитьс€ также член
особенно полезна ввиду того, что, как будет видно ниже, построение численного метода будет выполн€тьс€ на основе принципа баланса дл€ контрольного объема. единице объема относитьс€ также член  , который описывает скорость изменени€ соответствующего свойства в единице объема.
, который описывает скорость изменени€ соответствующего свойства в единице объема.






